


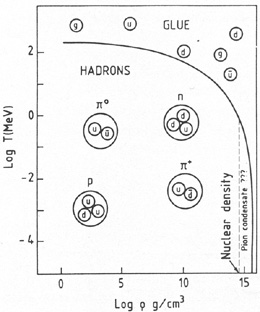
In the tradition of the chemists, we draw a two-phase diagram for these two states of nuclear matter: the hadronic (confined) phase of our everyday experience, with nucleons and mesons; and the glue (deconfined) phase with quarks and gluons (fig. 5). A phase transition contour-line separates the two phases as in the water-ice diagram.
|
Figure 5. Phase diagram of the quark-hadron phase transition. The abcissa is the nucleonic number density (nucleons minus antinucleons). |
Because of the fact that, at high temperature, pair productions
increases the actual density of the medium, the abcissa is best
labeled by a parameter other than the density. One chooses the baryon
chemical potential or equivalently the baryon density number, defined
as the difference in population between the nucleons and the
anti-nucleons per unit volume (but not divided by the photon density
number as in the cosmological parameter
 ).
).
On the right of the diagram, the hatched area named pion condensate refers to a hypothetical phase, characterized by a large population of pions in a Bose-Eistein condensate. The pions are bosons. Not limited by the exclusion principle, they could condensate in the lowest energy state available.
It is possible, but not certain, that at densities slightly larger than the nuclear densities, and rather low temperature, such a state could occur as an intermediate state between the hadronic phase and the glue. This state could be found in neutron stars.
Fig. 5 involves, in fact, two more or less simultaneous phase transitions. In parallel with the deconfinement transition, there is a so-called chiral transition. It corresponds to the fact that, at low temperature or low density, (lower left-hand size of the diagram) the quarks have an effective mass which they have lost in the higher right-hand side of the diagram. Massive quarks break the chiral symmetry of the lagrangian density. This symmetry is restored as soon as the effective mass disappears. Hence the name chiral transition. It is likely, but not certain, that the two transitions are simultaneous.
Another important question is the nature of the transition (or transitions). If it is second-order, the transition takes place as soon as the corresponding temperature is reached. There is no delay and no entropy creation. A first-order transition implies the possibility of overcooling, followed by a sudden non-adiabatic reheating, generating entropy. This appears to be the case for the quark-hadron phase transition.