In this section we describe the four estimators we have used to
compute the SFR from the luminosities of the
H
and
[OII]
3727 nebular lines, the UV luminosity and the FIR continuum.
The expressions used here are the ones we found most frequently referred
to in the literature. All expressions are for a Salpeter IMF (N(m)
m-2.35) with masses varying from 0.1 to 100
M
, solar
metallicity and continuous star formation. To convert the fluxes into
luminosities we used a Hubble constant of 70 km s-1
Mpc-1.
For the estimate of the SFR from
H luminosities we used
the expression given by
Kennicutt, Tamblyn and
Congdon (1994),
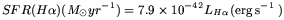
| (2) |
valid for a Te = 104K and Case B recombination, i.e. all the ionizing photons are processed by the gas.
3.2. From
[OII]3727 Luminosities.
The doublet [OII]3727 luminosity is used as
a SFR tracer for objects with redshift larger than 0.4 where
H is shifted outside the
optical range.
Unlike H,
the [OII]3727 intensity depends not
only on the electron temperature and density but also
on the degree of ionization and on the metallicity of the gas.
In practice a semi-empirical approach is used combining the
SFR(H) with the average
H /
[OII]3727 ratio given by
Gallagher et al. (1989)
using a sample of 75 blue galaxies and by
Kennicutt (1992)
from a sample of 90 normal and irregular galaxies.
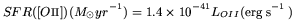
| (3) |
3.3. From UV Continuum Luminosities.
The UV continuum luminosity is used as a SFR tracer in objects with
redshift higher than 1-2. At these redshifts all strong emission lines,
apart from Ly, are
shifted outside the optical range.
In young stellar clusters, the UV spectrum is dominated by the continuum emission of massive stars. In evolutionary synthesis models of starbursts, after a short initial transient phase, the UV luminosity per unit frequency becomes proportional to the SFR,
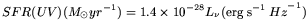
| (4) |
This equation is valid from 1500 to 2800 Å where the integrated
spectrum is nearly flat in F
for a Salpeter IMF, continuous mode of star formation and solar
metallicity. This region of the UV is not affected by the
Ly forest and the
contribution from old populations is still very small
(Kennicutt 1998,
Madau et al. 1998).
This SFR indicator though, is extremely sensitive to uncertainties in the reddening correction.
To transform the observed 60µm luminosity to SFR
we assumed that a fraction
of the
ultraviolet/optical flux emitted by stars is absorbed by
dust and reemitted as thermal emission in the far infrared
(10 - 300 µm). Work by, among others,
Mas-Hesse and Kunth (1991)
indicate that even for a small amount of reddening the
fraction is very
close to unity. This, plus the fact
that no dust extinction correction is necessary, justifies the
assumption that the FIR luminosity is an excellent indicator
of the total UV/optical emissivity of a galaxy.
Thus, the relation between the total FIR luminosity
and the star formation rate
(Kennicutt 1998) is
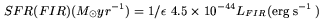
| (5) |
where the FIR luminosity is given by LFIR ~ 1.7 × L60µm [Chapman et al. 2000].
A difficult parameter to quantify is the fraction of ionizing photons that escape from the nebula. Heckman et al (2001) show that in five of the UV brightest local starburst galaxies the fraction of photons escaping is less than about 6% while Steidel, Pettini and Adelberger (2001) claim a higher escape fraction. Bearing in mind that the two samples differ, these results may not be contradictory. Tenorio-Tagle et al. (1999) have shown that the escape of photons from a starburst may be time dependent with a very large escape probability during the most luminous phases and little escape at other stages.
It is important to point out that if the dust and ionized gas distributions are similar, i.e. they coexist spatially, the FIR and the emission line luminosities will be similarly affected by the escape of photons. Thus, under this condition, the ratios of emission line fluxes to FIR flux are, to first order, independent of the fraction of escaped photons and therefore not very sensitive to variations in the photon escape from nebula to nebula.