We have applied the commonly used SFR estimators
to our reference sample of star forming galaxies.
Given that the estimators are all for the same IMF and stellar models
we do not expect these aspects to introduce any scatter.
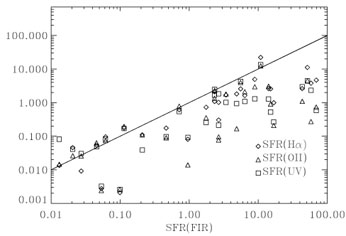
Figure 1 shows the
SFR(H
), SFR(OII) and
SFR(UV) plotted against
the SFR(FIR). Clearly the sample shows a correlation plus a large
scatter.
|
Figure 1. Standard SFR estimators vs. SFR(FIR). No extinction corrections were applied to the data. The solid line represents equal values. |
To simplify the analysis and simultaneously make use of the fact that
SFR(FIR)
is probably the best SFR estimator available, we will use in what follows
FIR normalized SFR, i.e. the SFR relative to SFR(FIR).
The FIR normalized SFR(H),
SFR(OII) and SFR(UV) are:
|
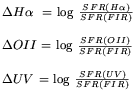
This is better seen in the distribution histograms of the normalized SFR as shown in Figure 2. As reference we included in parts a,d,g of the figure the normalized SFR computed using the observed luminosities. The central and right columns show the dust extinction corrected ratios using the MW and the Calzetti extinction laws respectively. The corrections were applied following the common methodology and are described in Appendix A.
|
Figure 2. Histograms of
the SFR rates given by the different tracers normalized to
the SFR(FIR).
In the left panels (a, d, g) no corrections were applied to the data.
In the central panels (b, e, h) we corrected the
H |
Our main conclusion is that irrespective of the extinction law applied,
the SFR(H) is close to
the SFR(FIR) while both SFR(OII) and SFR(UV) show a clear
excess. The excess is much larger for SFR(UV) than for SFR(OII) suggesting
a wavelength dependent effect, probably an extinction over-correction.
Bearing in mind that our reference sample has a large fraction of low
metallicity
and low extinction galaxies this result suggests that applying these
standard methods to estimate
SFR will systematically overestimate the SFR in samples at intermediate
and high redshifts where either SFR(OII) or SFR(UV) are used.
This result is in apparent contradiction with what has been found and
shown in Madau-type plots in recent years, where the SFR obtained from
UV and optical data are much lower than that obtained
from mm and sub-mm observations at intermediate and high redshifts. In
order to reach agreement between both determinations, fixed (and somehow
arbitrary) amounts of extinction have been
applied to the UV/optical data, because at the moment, the intermediate
and high redshift samples do not allow a reliable determination of
the dust extinction. It is worth noting that
Steidel et al. (1999)
applied a fixed correction to their sample that is close to the average
UV.
On a positive note we should indicate that the application of the reddening
corrections reduce considerably the scatter in all three normalized SFR
estimators as we will show below.
It is important to clarify the origin of the detected excess in the
extinction corrected
OII and
UV.
There is one effect that is not normally taken
into account, namely that the presence of an underlying young
stellar population with deep Balmer absorptions will bias the observed
emission line ratios towards larger Balmer decrement values, mimicking
the dust extinction effect. In the next section we will recalculate the
SFR for the different tracers but including an
estimation of the effect of an underlying population. We will also
estimate the effect of photon escape in
UV.
3727 and UV continuum by using the MW extinction curve.
In the right panels (c, f, i) the
H