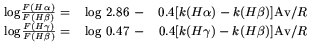A1. Dust Extinction Corrections to the
Continuum Fluxes
Calzetti and collaborators developed an empirical method to
estimate the UV extinction
(Calzetti, Kinney and
Storchi-Bergmann, 1994).
They found that the power-law index
 in the
ultraviolet defined as
F
in the
ultraviolet defined as
F


 is well correlated with the difference in optical depth between
H
is well correlated with the difference in optical depth between
H and
H
and
H defined as
defined as
 Bl
= ln{[F(H
Bl
= ln{[F(H )
/ F(H
)
/ F(H )] / 2.86} where
F(H
)] / 2.86} where
F(H ) and
F(H
) and
F(H ) are the intensities of the
H
) are the intensities of the
H and
H
and
H emission
lines respectively.
This correlation, which is linear and independent of the adopted
extinction law is given by,
emission
lines respectively.
This correlation, which is linear and independent of the adopted
extinction law is given by,
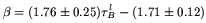
| (A1)
|
The parameter  is obtained by fitting the power law to the IUE ultraviolet spectra.
Calzetti et al. (1994) and
Meurer, Heckman and Calzetti
(1999)
values of
is obtained by fitting the power law to the IUE ultraviolet spectra.
Calzetti et al. (1994) and
Meurer, Heckman and Calzetti
(1999)
values of  are presented in Table 2 as well as our
estimate for CAM0840, CAM1543, TOL1247, ESO572 and MRK309.
are presented in Table 2 as well as our
estimate for CAM0840, CAM1543, TOL1247, ESO572 and MRK309.
The effect of reddening using different
dust spatial distributions can be estimated from Equation A1
by comparing ultraviolet with optical spectra.
Calzetti et al. (1994)
estimate the optical depth

 by solving the
transfer equation for five different geometries, uniform or clumpy dust
screen, uniform or clumpy scattering slab and internal dust.
The uniform dust screen constitutes the easiest case where the optical
depth is related to the visual extinction by
by solving the
transfer equation for five different geometries, uniform or clumpy dust
screen, uniform or clumpy scattering slab and internal dust.
The uniform dust screen constitutes the easiest case where the optical
depth is related to the visual extinction by
where E(B - V) is the colour excess and
k( ) is the
extinction law. For the other geometries, apart from the assumed
extinction law, the optical depth is a function of dust
parameters such as the albedo, the
phase parameter or the number of clumps.
After comparing synthetic extinction corrected spectra
with observations of emission line galaxies
Calzetti et al. (1994)
conclude that none of the adopted geometries
combined with the standard MW and LMC extinction laws
could explain the observed tight relation between
) is the
extinction law. For the other geometries, apart from the assumed
extinction law, the optical depth is a function of dust
parameters such as the albedo, the
phase parameter or the number of clumps.
After comparing synthetic extinction corrected spectra
with observations of emission line galaxies
Calzetti et al. (1994)
conclude that none of the adopted geometries
combined with the standard MW and LMC extinction laws
could explain the observed tight relation between
 Bl
and
Bl
and  and
proposed an empirical extinction law obtained from
IUE spectra of a sample of nearby starburst galaxies.
and
proposed an empirical extinction law obtained from
IUE spectra of a sample of nearby starburst galaxies.
Calzetti et al. (1994)
created 6 different templates averaging galaxies
with the same amount of dust (judging by their Balmer decrements).
The template with
 Bl =
0.05 is taken as the reference one (free of dust). An optical depth,
Bl =
0.05 is taken as the reference one (free of dust). An optical depth,
 n(
n( ), is calculated for each
template by comparing the observed fluxes,
Fn(
), is calculated for each
template by comparing the observed fluxes,
Fn( )
and
F1(
)
and
F1( ),
),
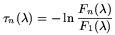
| (A2)
|
where the subindex 1 corresponds to the dusty free template and
the subindex n corresponds to the n template.
For each template a rescaled optical depth can be defined
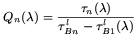
| (A3)
|
Averaging this quantity,
Calzetti et al. (1994)
found an extinction curve,
Q( )
which can be transformed to
k(
)
which can be transformed to
k( ) (e.g.
Seaton, 1979) by,
) (e.g.
Seaton, 1979) by,
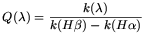
| (A4)
|
where the difference
k(H )
- k(H
)
- k(H ) is
given by the
Seaton (1979)
extinction curve. The observed ultraviolet flux is related to the
emitted one by,
) is
given by the
Seaton (1979)
extinction curve. The observed ultraviolet flux is related to the
emitted one by,
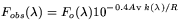
| (A5)
|
where
k( ) is given by
[Calzetti 1999]
) is given by
[Calzetti 1999]
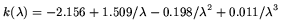
| (A6)
|
valid for the range 0.12 µm
<  < 0.63
µm.
< 0.63
µm.
The obtained extinction curve can be considered as
an average of the different dust distributions described by
Calzetti et al. (1994).
In order to correct the ultraviolet flux using this procedure it is
necessary to estimate Av from the observed
H / H
/ H ratios
and then apply Equation A6 to the observed ultraviolet fluxes.
Physically this correction is understood assuming that
the ionized gas is more affected by extinction than the
stars which are producing the observed UV flux
[Calzetti et al. 1994].
ratios
and then apply Equation A6 to the observed ultraviolet fluxes.
Physically this correction is understood assuming that
the ionized gas is more affected by extinction than the
stars which are producing the observed UV flux
[Calzetti et al. 1994].
No corrections were applied to the IR data.
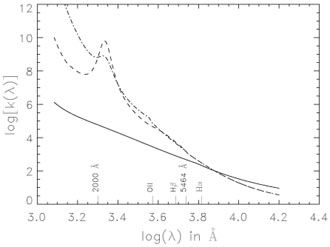
The different
extinction curves are plotted in Figure A1.
A2. Dust extinction corrections to the Emission Line
Fluxes
Extinction affects the emission lines in different degrees depending
on wavelength. Corrections are usually obtained from the observed
ratio of Balmer lines, the intrinsic ratio,
and an adopted interstellar extinction curve.
The ratio between the intensity of a given line
F( )
and the intensity of
H
)
and the intensity of
H ,
F(H
,
F(H )
can be expressed by:
)
can be expressed by:
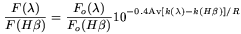
| (A7)
|
where the difference
k( ) -
k(H
) -
k(H ) is tabulated for different
extinction laws (Table A1).
The total visual extinction Av, depends on the observed object (see
Table 2).
The subindex o indicates the unreddened values.
We use as reference the theoretical ratio for Case B recombination
Fo(H
) is tabulated for different
extinction laws (Table A1).
The total visual extinction Av, depends on the observed object (see
Table 2).
The subindex o indicates the unreddened values.
We use as reference the theoretical ratio for Case B recombination
Fo(H )
/ Fo(H
)
/ Fo(H ) = 2.86 and
Fo(H
) = 2.86 and
Fo(H )
/ Fo(H
)
/ Fo(H ) = 0.47
[Osterbrock 1989].
The observed flux ratios can be expressed as a function of the
theoretical ratios and the visual extinction,
) = 0.47
[Osterbrock 1989].
The observed flux ratios can be expressed as a function of the
theoretical ratios and the visual extinction,
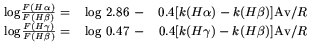
| (A8)
|
This Equation was used to analyze the presence of an underlying stellar
population in Section 5.1.




 )-k(H
)-k(H )
) )-k(H
)-k(H )
) 3727)
3727) in the
ultraviolet defined as
F
in the
ultraviolet defined as
F


 is well correlated with the difference in optical depth between
H
is well correlated with the difference in optical depth between
H and
H
and
H defined as
defined as
 Bl
= ln{[F(H
Bl
= ln{[F(H )
/ F(H
)
/ F(H )] / 2.86} where
F(H
)] / 2.86} where
F(H ) and
F(H
) and
F(H ) are the intensities of the
H
) are the intensities of the
H and
H
and
H emission
lines respectively.
This correlation, which is linear and independent of the adopted
extinction law is given by,
emission
lines respectively.
This correlation, which is linear and independent of the adopted
extinction law is given by,
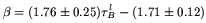
 is obtained by fitting the power law to the IUE ultraviolet spectra.
Calzetti et al. (1994) and
Meurer, Heckman and Calzetti
(1999)
values of
is obtained by fitting the power law to the IUE ultraviolet spectra.
Calzetti et al. (1994) and
Meurer, Heckman and Calzetti
(1999)
values of  are presented in Table 2 as well as our
estimate for CAM0840, CAM1543, TOL1247, ESO572 and MRK309.
are presented in Table 2 as well as our
estimate for CAM0840, CAM1543, TOL1247, ESO572 and MRK309.

 by solving the
transfer equation for five different geometries, uniform or clumpy dust
screen, uniform or clumpy scattering slab and internal dust.
The uniform dust screen constitutes the easiest case where the optical
depth is related to the visual extinction by
by solving the
transfer equation for five different geometries, uniform or clumpy dust
screen, uniform or clumpy scattering slab and internal dust.
The uniform dust screen constitutes the easiest case where the optical
depth is related to the visual extinction by
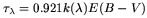
 ) is the
extinction law. For the other geometries, apart from the assumed
extinction law, the optical depth is a function of dust
parameters such as the albedo, the
phase parameter or the number of clumps.
After comparing synthetic extinction corrected spectra
with observations of emission line galaxies
Calzetti et al. (1994)
conclude that none of the adopted geometries
combined with the standard MW and LMC extinction laws
could explain the observed tight relation between
) is the
extinction law. For the other geometries, apart from the assumed
extinction law, the optical depth is a function of dust
parameters such as the albedo, the
phase parameter or the number of clumps.
After comparing synthetic extinction corrected spectra
with observations of emission line galaxies
Calzetti et al. (1994)
conclude that none of the adopted geometries
combined with the standard MW and LMC extinction laws
could explain the observed tight relation between
 Bl
and
Bl
and  and
proposed an empirical extinction law obtained from
IUE spectra of a sample of nearby starburst galaxies.
and
proposed an empirical extinction law obtained from
IUE spectra of a sample of nearby starburst galaxies.
 Bl =
0.05 is taken as the reference one (free of dust). An optical depth,
Bl =
0.05 is taken as the reference one (free of dust). An optical depth,
 n(
n( ), is calculated for each
template by comparing the observed fluxes,
Fn(
), is calculated for each
template by comparing the observed fluxes,
Fn( )
and
F1(
)
and
F1( ),
),
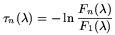
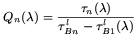
 )
which can be transformed to
k(
)
which can be transformed to
k( ) (e.g.
Seaton, 1979) by,
) (e.g.
Seaton, 1979) by,
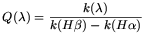
 )
- k(H
)
- k(H ) is
given by the
Seaton (1979)
extinction curve. The observed ultraviolet flux is related to the
emitted one by,
) is
given by the
Seaton (1979)
extinction curve. The observed ultraviolet flux is related to the
emitted one by,
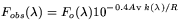
 ) is given by
[Calzetti 1999]
) is given by
[Calzetti 1999]
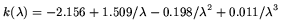
 < 0.63
µm.
< 0.63
µm.
 / H
/ H ratios
and then apply Equation A6 to the observed ultraviolet fluxes.
Physically this correction is understood assuming that
the ionized gas is more affected by extinction than the
stars which are producing the observed UV flux
[Calzetti et al. 1994].
ratios
and then apply Equation A6 to the observed ultraviolet fluxes.
Physically this correction is understood assuming that
the ionized gas is more affected by extinction than the
stars which are producing the observed UV flux
[Calzetti et al. 1994].
 )
and the intensity of
H
)
and the intensity of
H ,
F(H
,
F(H )
can be expressed by:
)
can be expressed by:
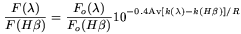
 ) -
k(H
) -
k(H ) is tabulated for different
extinction laws (Table A1).
The total visual extinction Av, depends on the observed object (see
Table 2).
The subindex o indicates the unreddened values.
We use as reference the theoretical ratio for Case B recombination
Fo(H
) is tabulated for different
extinction laws (Table A1).
The total visual extinction Av, depends on the observed object (see
Table 2).
The subindex o indicates the unreddened values.
We use as reference the theoretical ratio for Case B recombination
Fo(H )
/ Fo(H
)
/ Fo(H ) = 2.86 and
Fo(H
) = 2.86 and
Fo(H )
/ Fo(H
)
/ Fo(H ) = 0.47
[Osterbrock 1989].
The observed flux ratios can be expressed as a function of the
theoretical ratios and the visual extinction,
) = 0.47
[Osterbrock 1989].
The observed flux ratios can be expressed as a function of the
theoretical ratios and the visual extinction,