Annu. Rev. Astron. Astrophys. 1988. 26: 561-630 Copyright © 1988 by Annual Reviews. All rights reserved

8. ANGULAR DIAMETER OF RIGID RODS

8.1. The Standard Model

The theory of the angular diameter of a rigid rod at different distances in an expanding manifold was first worked out by Tolman (1930); it was discussed at greater length in his textbook (Tolman 1934) and also by Hubble & Tolman (1935) and was put into modem notation by Sandage (1972a), who emphasized the difference between galaxy metric and isophotal diameters.

Let rR₁ be the coordinate interval between the observer and a galaxy at light emission. Because light rays travel along null geodesics in the expanding manifold, the angle between the rays from the extremities of the source is constant along the light path (neglecting the very small gravitational scattering due to intervening matter; cf. Gunn 1967, Kantowski 1969). Hence, upon reception, the angular size of a source of intrinsic size y (which does not expand with the manifold) is

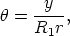
(43)

or, because R₀ = R₁(1 + z),

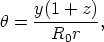
(44)

where R₀r is the coordinate interval of the source at the time of light reception given by Equation 30. Hence

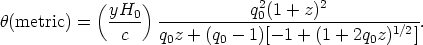
(45)

Consider again the two instructive cases of q₀ = 1/2 and q₀ = 0, whose R₀r values are given by Equations 22 and 26, respectively. Hence, for q₀ = 1/2,

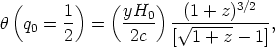
(46)

and for q₀ = 0,

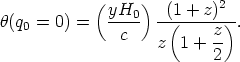
(47)

Galaxies do not have sharp edges; thus, measurements usually give isophotal diameters rather than metric. The two are not the same because in an expanding manifold, surface brightness is not constant with distance. The measured surface brightness is the received (apparent) flux divided by the apparent area, obtained by combining Equations 32 and 44, which gives

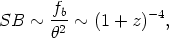
(48)

independent of R₀r. This means that Equation 48 is model independent, and therefore it does not depend on q₀. This famous theorem was first proved by Tolman (1930). Note that if the manifold is not expanding, Equation 32 has but one (1 + z) factor, and, since R₀ = R₁,

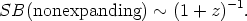
(49)

The difference between Equations 48 and 49 afford the well-known test (yet to be carried out properly) as to whether the manifold is truly expanding. Because isophotal diameters of galaxies differ from metric as a consequence of Equation 48, measurement of apparent diameters of galaxies to a given surface brightness cannot afford a test of Equation 48 (Sandage 1972a, Petrosian 1976, Tinsley 1976).

Suppose, in fact, that the manifold is not expanding and that the redshift is caused by some sort of energy decay of photons in the path to the observer. Although no mechanism has yet been proposed to avoid scattering of the photon beams in transit, and hence a blurring of distant images (not observed), nevertheless the predictions of this tired-light hypothesis are of interest.

Consider that the effect is linear with path length. Obviously then

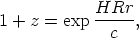
(50)

from which

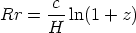
(51)

as a guess for flat space. In curved space the distance traveled is not Rr but rather R sin(HRr/c) for k = + 1 and R sinh(HRr/c) for k = - 1. Hence, in the case where the curvature factor is set to HR/c = 1 we have the possibilities

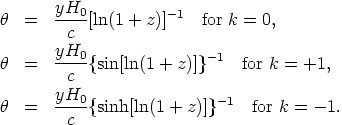
(52) (53) (54)

Return now to the expanding case of the standard model. It is instructive to expand Equation 45 in powers of z. The result is

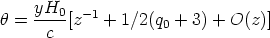
(55)

for all q₀. The leading term is z^-1, which can be shown also to be true for Equations 52-54. Hence both the standard model and the tired-light case require that angular metric diameters decrease as the inverse redshift for small z. This, of course, is the intuitive choice for a linear redshift-"distance" relation. [Note that in Segal's (1975) speculation, ~ z^-1.2 is the expectation]. The second-order term begins to be important for z > 0.2, causing the angular size to decrease more slowly than z^-1 for all models. The predictions from the exact equations are shown in Figure 11, together with the intuitive ~ z^-1 relation.

Figure 11. Theoretical angular size-redshift relations for q0 = 0 and q0 = 1/2 standard Friedmann models, and for three types of geometry for the tired-light speculation. The Euclidean ~ z-1 intuitive dependence is shown for purposes of comparison.

Hoyle (1959) was first to emphasize that for q₀ > 0, has a minimum at some finite z, larger than which the angular size increases. This is most easily seen by taking Equations 46 and 47 to their limits at large z. It is this that was believed to be the most direct geometrical test for the reality of expanding space. The effect has been sought in many observational tests (Section 8.3) but has not been found, raising what is the most serious doubt to date about the standard model because it questions whether the redshift is due to real expansion. Again, to save the phenomenon we must invoke evolution of the size of the standard rod in the look-back time. Before discussing the data at large look-back times, consider first the data at low redshift to test the leading term in the series expansions of Equations 45-47 and 52-54.