Copyright © 1988 by Annual Reviews. All rights reserved
|
| Annu. Rev. Astron. Astrophys. 1988. 26:
561-630 Copyright © 1988 by Annual Reviews. All rights reserved |
9.1. The Standard Model Prediction
The value of the redshift-distance ratio (i.e. the Hubble constant) was first set at H0 = 558 ± 10 % km s-1 Mpc-1 (Hubble & Humason 1931). Using this determination it was soon evident that the redshift of the galaxies is a characteristic of the Universe itself, rather than being simply a local phenomenon. The evidence is the order-of-magnitude agreement between the expansion time scale associated with H0-1 (which is 1.7 × 109 yr for H0 = 558) and the age of the Earth, known even at the beginning of this century to be of order 109 yr [Holmes (1913), and many times thereafter following Boltwood (1907); cf. Holmes (1946, 1947, 1949) and Jeffreys (1924, 1948, 1949) for the early literature].
The conclusion was strengthened when the age of the oldest stars in the Galaxy was shown to be of the same order (Sandage & Schwarzschild 1952). This followed the earlier, several-decade debate on two time scales for the Galaxy. Bok (1946) reviewed the multiple evidence for the long and short time scale. Note from his review that even in 1946, evolution of stars was considered to be up rather than off the main sequence, giving no characteristic signal in the HR diagram by which to date the stars. This difficulty prevailed until Trumpler's (1925, 1928) discovery of main sequence termination points was theoretically understood in the early 1950s with the introduction of chemically inhomogeneous stellar models.
A third time scale was proposed by Rutherford (1929) that permitted age dating of the chemical elements. Ages of several times 109 yr for uranium was close enough to the Hubble time to be startling. In modem times the theme has been integrated into a general history of events that have spread the elements made in stars everywhere that there is matter (Hoyle 1946, 1947, 1954, Burbridge et al. 1957), setting the foundations for the study of the chemical evolution of galaxies.
Although order-of-magnitude agreement of the three cosmic clocks
draws attention to the significance of the time-scale coincidence, a
more detailed inquiry requires precision in the measurements. The
standard model predicts the relation between the age of the Universe
T0, the Hubble constant H0, and
cosmological parameters q0 (or
0) and
. Many
representations of this parameter space exist, such as that of
Robertson (1955,
1963)
for a specific value of H0; of
Fowler (1987),
who generalized Robertson's parametrization by using
0 and
H0T0 as axes; or of Stabell &
Refsdal (1966,
their Figure 5) in the density,
q0 plane with H0T0
as parameter.
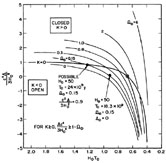
Figure 14 (from
Sandage & Tammann 1986)
is a diagram in the, H0T0,
plane with
0 as
parameter, plotted from the tables of
Refsdal et al. (1967)
following
Mattig (1958) and
Solheim (1966).
The well-known condition that T0 =
2/3H0-1 if
0 = 1 and
= 0
is marked by a crossed
circle. Two other data points are marked by filled circles at values
of H0 and T0 thought, in various
past discussions, to be
appropriate. The point to note about Figure 14 is that
H0T0, which is
in principle observable, permits
0 to be
determined if
is known (or
assumed); conversely, it permits
to be found if
H0T0 and
0 are
known. The special cut at
= 0 in the
diagram gives the
0 =
f (H0T0) relation calculated
earlier
(Sandage 1961a,
Table 8).
|
Figure 14. The time-scale test displayed in
the H0T0,
|