© CAMBRIDGE UNIVERSITY PRESS 1991

2.2. Hydrodynamic beam production

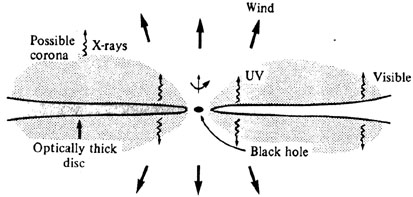
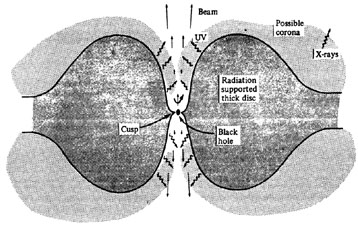
One large class of models assumes that magnetic fields do not play a dominant dynamical role in the extraction of energy from matter in the vicinity of a SMBH, nor are they important in the acceleration and collimation of beams (Fig. 1 and 2).

Figure 1. Relatively low accretion rates and weak magnetic fields yield optically thick, but geometrically thin discs.

Figure 2. High accretion rates can yield optically and geometrically thick radiation supported discs.

In these pictures, radiation from an accretion disc, either as direct thermal emission from its surface due to dissipation of energy within the disc, or as non-thermal reprocessed emission, is responsible for most of the observed activity. Such emission might occur in an optically thin corona above and below a disc or it might involve inverse-Compton scattering of photons off relativistic electrons. The question of the production and exact nature of the AGN continuum spectra will not be discussed in any detail in this chapter. In this area too, a wide range of explanations still seems possible (Begelman 1985, 1988; Stein & O'Dell 1985; Krishan & Wiita 1986; Zdziarski 1986; Stein 1988).

2.2.1. Thin accretion discs

It is likely that the gas finding itself in the vicinity of a SMBH will have significant angular momentum, and if the mass infall rate is less than about _E / 2, but is not exceedingly small, then it should evolve in such a way that most of the mass spirals inward in a thin disc while most of the angular momentum wends its way outward (e.g., Shakura and Sunyaev 1973). Under these circumstances the great majority of the released binding energy can be radiated away from the disc and it can remain geometrically thin (Fig. 1). The assumption that the total disc mass is much less than that of the central body, along with the thinness of the discs, implies that their vertical and radial structures can be approximately decoupled. Although both molecular and radiative viscosities are far too small to drive significant accretion or release much energy, the assumption that turbulent motions and/or tangled magnetic fields can and will produce important macroscopic viscosities has been widely accepted. The standard models for accretion discs grossly simplify the picture and assume that the shear stress is related to the pressure by a constant viscosity parameter: t_r = ^*P. Nevertheless, our lack of a fundamental understanding of these processes has precluded the formation of fully self-consistent models.

In the case of a Schwarzschild black hole, the last stable circular orbit around a body of mass M is at (e.g., Lynden-Bell 1969)

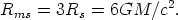
(3)

The formula for the angular momentum per unit mass on a circular orbit is

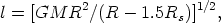
(4)

while that for the binding energy of a mass m in such an orbit is

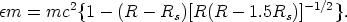
(5)

The maximum efficiency with which mass can be converted to energy during the accretion process is equal to the binding energy of the last stable circular orbit; using equations (4) and (5) one has

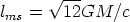
(6)

and

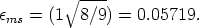
(7)

Unstable orbits can exist down to the marginally bound radius, R_mb = 2R_s, where = 0.

For a rotating (Kerr) BH, its angular momentum produces an effective repulsion of material orbiting in the same sense with the result that the radius of the last stable orbit is reduced and the binding energy is increased. It is natural to expect that even if a BH somehow formed without net angular momentum, it would be spun up via the addition of angular momentum from the accreted matter. It is believed that this process will not continue until the BH becomes an extreme Kerr BH, with angular momentum parameter a = 1, because of the preferential capture of counter-rotating photons emitted by the accreting matter; rather the spin-up should halt at a = 0.998 (Thorne 1974), where the efficiency ~ 0.32.

Although a wide range of temperatures would be characteristic of the emission from the material spiralling into a SMBH, the maximum flux and highest temperatures both occur at only a few R_s. Such a disc has a maximum temperature of roughly (Begelman 1985)

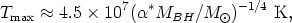
(8a)

if radiation pressure dominates, while if the disc is dominated by gas pressure then

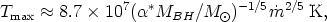
(8b)

where / _E. Gas pressure should be more important if 0.2(^* M_BH / M. As long as the electron scattering opacity dominates free-free opacity and the disc is optically thick then the observed radiation will be a diluted blackbody with a temperature closer to

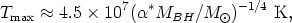
(9)

Evidence for the existence of accretion discs around SMBHs of between ~ 2 × 10⁸ and 4 × 10⁹ M has come from detailed analyses of the IR-UV spectra of six powerful QSOs (Malkan 1983). Power laws plus single blackbody components do not fit the observed continua well, while the broader additions to the spectra that arise from theoretical models of geometrically thin and optically thick accretion discs do a good job of modelling the "big blue bumps", or near UV excesses above many quasar spectra. However, the weak dependences of T_disc on M_BH, M and ^* mean that any values for disc properties or black hole masses derived from QSO spectra must be treated gingerly. Despite this caveat, recent fits by Madau (1988) and Sun & Malkan (1988) to AGN spectra are impressive indeed.

Another approach towards determining SMBH masses involves comparing X-ray variability and emission linewidths (cf. Section 2.1.1 - .2). There is a good correlation between the shortest observed X-ray variability time, assumed to be proportional to the hole's mass, and a virial mass (derived from velocities obtained from [O III] linewidths and distances obtained from ionization parameters) if 0.003 L / L_E 0.03 for QSOs and Seyfert 1's (Wandel & Mushotzky 1986). However, this analysis depends on uncertain selection effects and many reasonable, but by no means fully established, assumptions; while suggestive, it cannot yet be considered definitive.

Some of the variability might be due to unstable modes of oscillation in thin accretion discs. A long-wavelength instability that leads the inner parts of thin discs to break up into alternately dense and rarefied rings was discovered quite early (Lightman & Eardley 1974), and was later shown to be the limiting case of one of two families of instabilities to which ordinary ^*-discs were subject (Shakura & Sunyaev 1976); the other thermal instabilities have growth rates nearly independent of wavelength. Radiation pressure dominated thin discs are also unstable to axisymmetric instabilities unless the shear is proportional only to gas pressure and not the total pressure (e.g., Camenzind et al. 1986).

Although thin accretion discs obviously define preferred directions for emission of matter that could then be collimated into beams, no well-developed models for beam production in the absence of dynamically controlling magnetic fields have been proposed for them. If thin discs are capable of generating significant outflows then they probably must do so through winds expelled from a corona above and below the disc. Such a corona could be produced through mechanical heating such as the dissipation of shocks or turbulence (e.g., Liang & Price 1977). Alternatively, X-rays emitted from the very central region could Compton heat more distant portions of a thin disc which flares in thickness at larger radii (cf. Fig. 1); this might then produce a wind (Begelman, McKee & Shields 1983). It has been shown that a wind emerging from the outer portions of an accretion disc may be able to assist in the collimation of a more intense beam emitted from the very central portions (Smith & Raine 1985; Sol et al. 1989), which in turn is probably generated through one of the mechanisms to be discussed below.

2.2.2. Radiation supported thick accretion discs

When the accretion rate approaches and surpasses _E not all of the energy generated by viscosity within the disc can be radiated from the surface of a thin disc. Two distinct possibilities for the structure of the accreting material then emerge: (1) the angular momentum is lost very efficiently through very strong turbulence or some other mechanism and then the accretion flow becomes quasi-spherical; (2) if the value of ^* is very small then the angular momentum loss remains gradual and the direction defined by the spin axis of the black hole and infalling gas retains its influence. The first possibility implies that essentially spherical supercritical winds are likely to be driven away from the SMBH (to be discussed in Section 2.2.3); the latter implies that a geometrically thick accretion disc, supported by radiation pressure and rotation in comparable amounts, will form around the SMBH (Lynden-Bell 1978; Paczynski & Wiita 1980); see Fig. 2.

2.2.2.1 Thick disc structure

h/r, is proportional to , it is clear that such supercritical discs would be geometrically thick, and are often called tori or doughnuts. For discs to be in hydrostatic equilibrium (i.e., |v_r| << c_s, the local speed of sound)

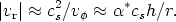
(10)

For thin discs h/r << 1, so ^* of order unity is acceptable, but for thick discs, h/r 1, so ^* << 1 is necessary. Even at subcritical accretion rates, the clumping instabilities that affect thin discs could imply a time-averaged bloated structure in the inner regions (Paczynski & Wiita 1980). The recognition that radiation supported rings or tori of fluid could exist around BHs if the fluid had a non-Keplerian angular momentum distribution, and that the inner radii of these discs could penetrate R_ms (e.g., Abramowicz et al. 1978), led to the suggestion that accreting material could form a pair of very steep vortices along the rotation axes. Such vortices could conceivably lead to collimated jets in QSOs and radio galaxies (Lynden-Bell 1978).

Since the vertical and radial parts of the disc structure cannot be separated, complete detailed models cannot be constructed analytically, and even numerical simulations (Hawley et al. 1984; Eggum et al. 1985; Clarke et al. 1985) must involve major simplifications. Nevertheless, it was shown that the boundary of such thick discs could be constructed with one free function (Paczynski & Wiita 1980; Jaroszynski et al. 1980). For example, the specific angular momentum (l) or equivalently the disc thickness (h), could be specified as a function of cylindrical radius (r), instead of just specifying a single free variable (usually chosen as ^*) for a thin disc. Even though l (r) is a free function, basic stability requirements greatly restrict its allowed forms. Of course, in the presence of a BH, the appropriate relativistic generalizations of angular velocity and angular momentum should be used, e.g.,

(11)

and, for a static distribution, the angular momentum is not constant on cylinders, but rather on curved Von Zeipel surfaces (Chakrabarti 1985a).

The large radiation pressure forces the rotational force to provide extra outward support close to the BH so that the specific angular momentum in a thick disc starts out at a value above the relativistic generalization of the Keplerian value, and rises more slowly than does l_Kep; in the innermost regions of the accretion disc l constant must be true (Abramowicz et al. 1978). The two curves intersect at the point of maximum pressure and density in the equator of the torus, which typically lies at only a few R_s. Beyond that distance l < l_Kep, but at large distances they should asymptotically agree, and the thick disc would eventually merge onto a "thin" disc of constant thickness 2R_s. As long as the equation of state is assumed to be barotropic (i.e., pressure solely a function of energy density) then Chakrabarti (1985a) shows that stability requirements and the above considerations imply that a very reasonable parameterization is

(12)

where 0 n 1/2, and l_in is the specific angular momentum at the inner edge, r_in of the disc. That edge, which locates the cusp through which matter falls into the BH, must lie between the closest marginally stable orbit, R_ms (which is 3R_s for Schwarzschild BHs) and R_mb.

The most surprising claim from these analyses was that these radiation pressure supported discs can evince super-Eddington luminosities while remaining in mechanical equilibrium. These models assume that the radiative flux from the surface of the disc is locally near the Eddington rate, i.e., F_rad = cg_eff / , and then the integrated flux from the highly non-spherical surface can exceed L_E. Thus thick, radiation supported disc models may be of relevance to quasars, Seyferts and BL Lacs, but almost certainly cannot be the primary explanation for optically faint radio galaxies.

As rises the cusp at the inner edge of the disc proceeds inward from R_ms towards R_mb, and the radiated luminosity can increase beyond L_E. However, because drops concomitantly th1e accretion rate rises faster than L (Paczynski & Wiita 1980). It turns out that radiation emitted from a torus around a rapidly rotating Kerr BH is ~ 30% higher than that from a disc around a Schwarzschild BH with the same accretion rate (Jaroszynski et al. 1980). Even though the existence of thick discs does depend on relativistic effects, i.e., r_in < R_ms, some useful approximations can be made using a purely Newtonian treatment, where the key parameter is the ratio of inner and outer disc radii. The maximum luminosity (for non-rotating BHs) is (Abramowicz et al. 1980)

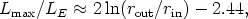
(13)

as long as r_in/r_out < 0.01, with r_out the radius at which the disc is effectively geometrically thin.

2.2.2.2 Consistency and stability

Relatively simple thick disc models can be self-consistent only if: (1) the mass of the disc is small compared to the mass of the BH; (2) viscous processes, not nuclear fusion, generate the vast majority of the energy; and (3) the disc remains in mechanical equilibrium. Condition (1) is probably violated if M_BH > 10⁷ M (Wiita 1982b), although that does not preclude more complicated models where the disc's self-gravity is not ignored. Such models are possible, and probably not very much different in the inner regions of the disc, but values of M_disc / M_BH as low as ~ 0.01 can imply significant changes in the structure of the outer disc (Abramowicz et al. 1984). Allowing for the changes in disc structure induced by the disc's own gravity this constraint probably only rules out radiation supported thick discs around extraordinarily massive (> 10¹¹ M) BHs (e.g., Begelman 1985).

Simple thick discs around objects of less than 100 M are unlikely, since fusion reactions would then probably generate more energy than viscous dissipation (Wiita 1982a, b). As far as AGN are concerned constraint (2) probably only serves to keep the temperature of the core of the disc below ~ 10⁸ K (Begelman 1985). The possibility that significant nuclear fusion could occur in accretion discs in AGN without leading to disruption has recently been explored by Chakrabarti et al. (1987); they show that p-p nucleosynthesis could proceed smoothly as an important energy source but that CNO or helium fusion is not likely to be stable. Fully self-consistent discs with ongoing fusion reactions ought to be calculated before we can be confident that they play no significant role.

The stability of thick discs is a most important question that has received tremendous attention over the past few years. Too high an effective value of ^* would imply rapid collapse of the disc. But a direct application of constraint (3) is extremely model dependent in that our lack of knowledge of the applicable viscosity under these conditions means that we cannot make any convincing argument in either direction concerning this point (Wiita 1982b; Begelman 1985). A thick disc could be disrupted if material jets driven by radiation pressure from its funnels were too efficient in removing matter from the disc; however, this process is probably not tremendously important (Narayan et al. 1983), although here too more detailed calculations are needed.

Recently Papaloizou & Pringle (1984, 1985) have discovered a set of virulent instabilities that apparently afflict thick accretion discs. These instabilities are global and non-axisymmetric (and thus were overlooked in earlier, purely axisymmetric analyses); they grow on dynamical (orbital) time scales. The original calculations were confined to constant entropy, incompressible tori with constant specific angular momentum (Papaloizou & Pringle 1984; Blaes 1985a; Hanawa 1986) and so were not clearly important for "real" cases. Extensions of this work showed that even incompressible tori are subject to the same problem (Blaes 1985b). The physical nature of the instability was clarified when it was shown that even uniform entropy thin rings with arbitrary angular momentum distributions were subject to this type of non-axisymmetric instability. The rapid growth of the instability, however, demands a good reflecting boundary at either the inner or outer edge of the disc (Goldreich & Narayan 1985), which may well be lacking. Although all of the above work was done in a Newtonian framework, similar results were shown to hold when a "pseudo-Newtonian" (Paczynski & Wiita 1980) potential was employed (Blaes & Glatzel 1986), and the necessary fully relativistic framework has been given (Blandford et al. 1985) although it is not yet completely explored.

Further analysis indicated that the most general mode is a combination of the modes described above which are driven by compressibility and additional Kelvin-Helmholtz-like instabilities excited in regions of the disc where there were maxima in the ratio of vorticity to surface density (Papaloizou & Pringle 1985). The most detailed analytic treatment to date clarifies and changes the physical nature of these instabilities (Goldreich et al. 1986). It now appears that the modes are best understood as edge waves propagating backwards at the inner edge of the torus and forwards at the outer edge; they are coupled together at the corotation point which must occur at the pressure maximum. These modes can grow most rapidly when the torus is incompressible since the edge is sharply defined, but in a more realistic compressible case such modes can also propagate along the "natural soft edge provided by the density gradient" (Goldreich et al. 1986). However, the growth rates are somewhat less for thicker tori. For (Newtonian) angular velocity variations as r^-q, q = 3/2 corresponds to Keplerian rotation, while q = 2 corresponds to constant specific angular momentum. The rapidly growing dynamical modes apply for 3 < q < 2.

The importance of these instabilities has recently been demonstrated by numerical simulations (Zurek & Benz 1986; Hawley 1988). If an isentropic pressure supported torus is initiated with a constant specific angular momentum distribution then it very rapidly becomes unstable. But non-linear effects that cannot be treated by analytical computations come into play (e.g., Kojima 1986), and such instabilities appear to provide an effective viscosity which rapidly redeploys the angular momentum into a distribution with q ~ 3 (Zurek & Benz 1986). Much more work on this question is required, as relativistic effects and wider ranges of initial assumptions must be incorporated. But at this point is appears reasonable to conclude that the dynamical instabilities do not necessarily disrupt thick accretion discs; rather, they may force them into very specific forms dictated by the viscosity provided by that self-same mechanism.

A very important recent calculation has finally included the effect of accretion from the thick tori onto the BH on the growth of these instabilities, albeit only in the two-dimensional approximation of an accretion annulus (Blaes 1987). It is found that when the inner edge of the flow crosses the critical cusp radius the flow into the hole is transonic; this removes the strong reflection necessary for the instability and stabilizes all of the modes that could be calculated. This is a preliminary result which might overstate the stabilizing effect of accretion on tori with respect to the full three-dimensional situation, but is of great interest and clearly must be amplified upon.

2.2.2.3 Beam formation

The basic geometry of thick discs, with their rather narrow funnels containing an extremely high radiation density, immediately suggested a natural way to produce beams (Lynden-Bell 1978; Paczynski & Wiita 1980). Early calculations using these models were promising, in that test particles within the funnel are definitely in a non-stationary zone: they either must fall into the BH or they must be expelled, and this cut-off point occurs very far down into the funnel. The net flux of radiation within the funnel is directed both upward and inward towards the axis, so both acceleration and collimation are to be expected.

The acceleration of a particle by radiation pressure within a beam is determined by (Jaroszynski et al. 1980; Abramowicz & Piran 1980)

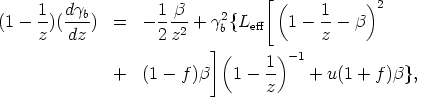
(14)

where u is the energy density of the uncollimated radiation, z is the height above the equator in units of R_s, 0 f 1 is a factor describing the deviation of u from isotropy, and L_eff is the effective outgoing luminosity, approximately given by

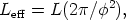
(15)

with the opening angle of the funnel and L the total luminosity of the radiation emitted within the funnel. Because particles accelerated in the lower parts of the funnel feel the isotropic component of the radiation field as a drag force, efficient acceleration only starts to occur at a distance up the funnel of ~ 100R_s and a terminal velocity is reached at heights of a few times that value (Abramowicz & Piran 1980). Mildly relativistic velocities ( 0.8) are achieved for ordinary plasma in a wide variety of models constructed using different disc models (Abramowicz & Piran 1980; Sikora & Wilson 1981) but if the plasma is of lower mass, i.e., predominantly electrons and positrons, then _bs around 3 or 4 are possible. However, this type of beam is not terribly well collimated, with half opening angles typically exceeding 10°. This is because the particle trajectories tend to diverge from the paths determined in the often narrower funnels once above the point where the funnels spreads out. Such optically thin beams, based on test particle calculations, cannot carry a large fraction of the total disc luminosity (Sikora & Wilson 1981; Narayan et al. 1983). Although the fluxes and Lorentz factors involved may not be adequate for all types of jets and the collimations are not as good as often seen, this type of beam model may still have astrophysical significance is some cases (Wiita et al. 1982).

Computations of optically thick flows within accretion funnels are far more difficult, especially because at some point the distinction between funnel wall and accelerated material becomes fuzzy. Crude models that include the continuous loss of hot mass into the funnel from the walls and allow for moderately optically thick flows have been produced (Calvani & Nobili 1983; Calvani et al. 1983); they yield extremely hot beams, with 10⁷ K T_b 10⁹ K with _b ~ 2 for ordinary plasma. However, these models rely upon considering the flow in a one-dimensional approximation and also require arbitrary, and very unsure, assumptions concerning mass loss from the funnel walls, so any conclusions must be regarded as extremely uncertain. More detailed radiation transport calculations in mildly optically thick funnels have recently been calculated and distinctly anisotropic emission and polar outflows are produced (Madej et al. 1987). Still, these preliminary results do not indicate that extremely high velocities or very narrow beams are likely to emerge.

If the flows are extremely optically thick then the radiation gas mixture acts like an adiabatic fluid with polytropic index, = 4/3, and such an outflowing mixture in a funnel could conceivably reach very high outflow velocities if the sonic point is close enough to the SMBH (Fukue 1982). However, Lu (1986) has shown that while extremely relativistic terminal velocities are possible under these idealized circumstances they can only be achieved if the enthalpy of the gas is extraordinarily high. Only if the sonic point for the flow is within 4R_s can exceed 0.9, and it is extremely difficult to see how such a situation can possibly be attained. A general treatment by Chakrabarti (1985b, 1986) has also shown that in principle very rapid, very narrow beams can form, where the collimation is primarily engendered by the angular momentum contained in the fluid approaching the SMBH. These rotating wind solutions are very interesting but so far have employed very specialized disc models. They deserve to be tied to more detailed disc models, so the possibility that such narrow beams can really form in this way can be fairly evaluated.

Numerical hydrodynamical models for the formation of thick accretion discs and possible beams have been attempted, but in all cases significant approximations have had to be made so as to keep the computations tractable. Eggum et al. (1985) neglect general relativistic effects and assume an approximately constant value of ^* ~ 0.1 for an = 4 calculation for an M = 3M BH. They find that complex convection cells form inside the disc and block accretion flow along the disc midplane and the majority of the radiation is trapped and swallowed by the BH. Low density material near the photosphere is accelerated to ~ 0.3 in a conical outflow and the outgoing mass flux is very small. Calculations incorporating full general relativistic effects, but assuming the infalling matter has fixed values of specific angular momentum and neglecting all viscosity save that generated by numerical shock smoothing have been performed by Hawley (1985). He finds that if l is in the right range to allow accretion tori to form, a complex series of shocks and convection patterns are set up, which do apparently stabilize in an axisymmetric computation. Published results to date do not yet clarify the likely strength and opening angle of ejected matter, because, among other reasons, the computational zone does not extend far enough away from the BH.

In conclusion, thick, radiation supported accretion discs do have many points in their favour, and, despite the uncertainties caused by the discoveries of the Papaloizou-Pringle instabilities, they probably do occur if circumstances are such that large amounts of matter rain upon a BH. But note that if the arguments of Wandel & Mushotzky (1986) are borne out by further data and analysis, then such supercritical conditions are, at best, infrequent. Nonetheless, assuming that supercritical mass flows are available then there is also little question that radiation supported tori can produce moderately powerful, reasonably well collimated, mildly relativistic beams. However, observations of extremely narrow jets (at least on much larger scales) and the probability that Lorentz factors of greater than five are needed for some sources, mean that they are not the most promising explanation of the origin of such jets.

2.2.3. Windy models

Assorted models for powerful, rapid outflows have been proposed that in principle are independent of the details of an accretion flow. While none of them have received the attention of other ideas discussed in this chapter, these approaches are intriguing.

2.2.3.1 Funnel winds

Models for beam formation based upon results taken from solar wind theory have also been suggested for AGN (Ferrari et al. 1984a, b, 1985, 1986). These wind type flows can be quasi-spherical or confined within funnels, either produced by radiation supported tori (Section 2.2.2) or ion supported tori (Section 2.3.1); the key new feature is that multiple critical points are found to exist in the flow so that the solutions are steady and transonic, but very possibly multiple. Details of this picture are too complex to develop here, but a summary of the exciting results is worthwhile. In a simplified Newtonian version of this wind scenario, a highly supersonic flow can be generated if the flow tube shape varies appropriately and there is significant non-thermal deposition of energy within the fluid (Ferrari et al. 1984a). In particular, if the flow expands rapidly, as it might on emerging from the outer part of an accretion disc funnel, and it is also acted upon by electromagnetic, plasma or MHD waves, then transonic solutions are easily achieved just above or within the disc region. Changes in the cross-section would naturally result in shock discontinuities and associated compression, heating, and particle acceleration (cf. Chapter 9). An important result is that degenerate solutions can exist; i.e., for given boundary conditions while there is always one continuous solution there are often additional discontinuous solutions. Which branch is followed depends sensitively on the history of the flow, indicating that numerical experiments must be treated very cautiously.

This basic idea was expanded to include relativistic motion of an optically thin wind within an accretion funnel (although the temperature is assumed to be non-relativistic) and again multiple critical points are found (Ferrari et al. 1985). Many solutions of the quasi-two-dimensional relativistic Navier-Stokes equations can be found if a lengthy, albeit reasonable, list of assumptions is made. A key claim is that if L < L_E such flows are typically accelerated to mildly relativistic velocities ( 0.28) very close to the disc. Perhaps more interestingly, for hot winds emerging from funnels of highly supercritical thick discs, > 0.9 is possible, in contrast to the conclusions based upon purely radiative acceleration discussed in Section 2.2.2.3. Another interesting result is that an increase in the collimation of the radiation field leads to the critical points descending deeper into the funnel even though the acceleration is not purely radiative; such a shift both increases the geometric collimation of the beam by the funnel and increases the amount of energy the radiation field deposits into the supersonic part of the flow, thereby raising the terminal velocity. However, it must not be forgotten that these calculations depend on a large number of parameters and simplifications; in particular, only essentially isothermal flows are accelerated very efficiently, and the relevance of these assumptions to real situations is anything but clear. Nonetheless, when rotational (cf. Chakrabarti 1985b) or magnetic (e.g., Siah 1985; Clarke et al. 1986; Siah & Wiita 1987) effects are included the collimation and acceleration which are essentially produced by this wind-type acceleration should be even better.

2.2.3.2 Supercritical Comptonized winds

Another type of wind scenario assumes that no funnel can survive if the accretion rate is high enough. Rather, the BH would essentially be smothered (Shakura & Sunyaev 1973; Meier 1982) and a quasi-spherical wind could be expelled (Becker & Begelman 1986a, b). Applications of this type of wind to AGN are motivated by the evidence emerging from some Broad Absorption Line Quasars that mass outflows exceeding _E are probable (e.g., Drew & Boksenberg 1984). If the scattering optical depth below a critical sonic radius, r_c, is so high that the flow velocity of the wind exceeds the diffusion velocity of the photons then the radiation is trapped inside r_t and is advected along with the flow. Such supercritical winds require a mass loss such that

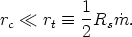
(16)

The great majority of this radiation is then available to accelerate the wind through adiabatic cooling. Under these circumstances the radiation and matter will be coupled by multiple Compton scatterings and must essentially act as a single adiabatic fluid.

These models depend upon the assumption that nearly all of the energy is deposited in a thin layer of matter near the base of the flow, at r_i, perhaps through turbulent or shock dissipation. As long as r_i << r_t significant acceleration and a relativistic terminal velocity can be achieved. The luminosity seen by an observer at infinity is roughly given by (Becker & Begelman 1986b)

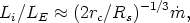
(17)

and this can greatly exceed L_E as long as the supercritical outflow traverses a sonic point which is deep in the relativistic potential. The emergent spectrum can have a colour temperature consistent with those argued for QSO blue bumps while the Compton scattered hard tail can be made to fit the overall QSO X-ray spectra.

This approach is indubitably interesting, but does require rather extreme conditions that are not likely to be frequently encountered. This is particularly true in that the mechanical heating assumed is not likely to be very efficient, thereby implying a tremendous excess supply of energy is required. These calculations have also been performed assuming spherical symmetry, so that it is not at all clear if this idea can have any productive role in beam formation.

A brief mention of a related way in which radiation pressure might drive jets is in order. If the fluid is so optically thick that radiation is trapped and somehow P_rad > _matter c² then relativistic outflows could be produced in a "cauldron" (Begelman & Rees 1983). Any collimation achieved would depend upon the distribution of the matter at larger scales and is unlikely to be very good.