© CAMBRIDGE UNIVERSITY PRESS 1991

2.3. Magnetohydrodynamical models

The other major category of central engine and beam models consider the magnetic fields to be of dominating importance. The existence of dynamically significant magnetic fields on relevant scales is consistent with polarization measurements (cf. Sections 4.3.2, 4.3.3 and 3.1), and many explanations for the continuum spectrum, such as the synchrotron self-Compton model, also require B ~ 10^{2 - 4} gauss in the region very close to the SMBH. A detailed understanding of magnetohydrodynamical processes under such extreme conditions is obviously even more difficult to obtain than a similar level of understanding of purely hydrodynamical events, but a great deal of progress has been made over the past few years, and a few plausible scenarios have emerged.

2.3.1. Extraction of the black hole's rotational energy

As long as one ignores quantum evaporation, which is certainly a reasonable thing to do when considering SMBHs, a Schwarzschild BH is purely a sink of mass and energy; however, the same is not true for Kerr-Newman BHs. Energy can be extracted from a rotating BH if particles and/or fields penetrate its ergosphere, the region between the event horizon and the static limit for rotating and/or charged BHs (Penrose 1969). In principle it is possible to remove energy equivalent to a significant fraction of the mass of an extreme (a = 1) Kerr BH, leaving an irreducible mass of M_ir = M / 2; the available energy is thus an immense [(2 - 1) / 2]Mc², or 29%, of the BH's rest-mass energy. This energy is most easily understood as being extracted if a particle breaks up within the ergosphere, with one piece falling into a negative energy state of the BH, while the other emerges with more energy than the initial one had to begin with; after such an event the BH is left rotating less rapidly.

2.3.1.1 "Pure" Penrose processes

Applications of this idea in astrophysically useful situations are few and they are all based upon greatly simplified pictures. It has been analyzed in the context of "inverse-Compton" (Piran & Shaham 1977) and pair production (Kafatos & Leiter 1979) mechanisms near rapidly rotating black holes. An infalling photon that collides with a proton or electron fairly deep within the ergosphere can knock the particle into a negative energy orbit and emerge with a high energy as seen by an observer at infinity, but the huge flux of -rays produced by this process does not agree with observed AGN spectra. It is also a problem that in the absence of large electromagnetic fields, such a process could only work if the incident particle starts with a relativistic velocity, which means the efficiency is very low. It has recently been pointed out that if a BH is immersed in an electromagnetic field then negative energy states can be opened up to even slowly moving particles (Dhurandhar & Dadhich 1984; Wiita et al. 1983) and the efficiency of this process is not necessarily negligible (Wagh et al. 1985). The efficiency of this "magnetic Penrose process" is given roughly by (Parthasarathy et al. 1986)

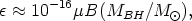
(18)

with µ the charge per unit mass of the escaping particle. Although is essentially unity for reasonable values of the parameters if the disintegration is near the static limit, no convincing self-consistent model of the particle break-up picture has yet emerged. Further, it appears as if the emitted particles tend to be concentrated towards the equator and not the poles of the BH, so direct beam formation by this mechanism is unlikely.

2.3.1.2 Black hole magnetodynamics

A more promising way to extract the energy of a rotating BH via magnetic fields exists, and one particular model will be discussed in Section 2.3.2. Although even the simplest general set of BH MHD solutions depends upon an extraordinarily complicated evaluation of the equations of axisymmetric magnetohydrodynamics in a curved background spacetime, several things are the same in all types of magnetospheres. Phinney (1983) has illustrated the basic analogy between: (a) a conductor rotating in a uniform magnetic field with and without surrounding plasma and the subsequent induced charge density and energy loss and (b) a BH surrounded by a magnetic field and plasma. In the absence of an external plasma and currents, an electric field of magnitude aBR_s² / (Mr²) and an azimuthally circulating Poynting flux are induced; however, no net radiation escapes if the field is aligned with the spin axis. If the magnetic axis is misaligned by an angle then the BH feels an aligning torque and surface currents dissipate energy on the horizon at a rate proportional to (_BH BR_s² sin)² (Damour 1978) and the loss can be made analogous to that of an ordinary rotating conductor if the surface impedance of the horizon is identified as Z_H = 4 / c = 377 ohms.

Allowing a circuit, presumably in the form of an accretion disc with associated currents, to interact with the BH means that its rotational energy can be tapped and delivered as work at large distances. In one simplified picture the disc acts like a unipolar inductor, generating an electric field in the inertial frame and driving a DC Poynting flux. If charged particles of either sign can leave the disc to form a force-free magnetosphere above and below it then, in classical notation,

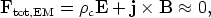
(19)

with a space charge _c yielding the divergence of E and the current distribution j modifying B (Blandford 1976; Blandford & Znajek 1977). A related view of this situation is that the large electric potentials actually cause a vacuum breakdown which generates electron-positron pairs which in turn set up the force-free magnetosphere. If this is physically possible then the energy and any generated beams apparently can be focused along the rotation axes.

However Phinney (1983) argues that if the accretion disc produces any significant quantity of > 1 MeV -rays then the electron-positron pair density produced by photonic collisions in the magnetosphere would exceed that allowed for a force-free magnetosphere. Under these circumstances a perfect MHD approximation becomes applicable and drift forces transfer energy from fields to bulk kinetic energy. While the complexity of the MHD equations is such that no complete solution is likely to be found, some general results can be obtained. This is because four integrals of the motion exist (the energy at infinity/unit rest mass; angular momentum at infinity/unit rest mass; ratio of rest mass to magnetic flux in a flux tube; and the angular velocity of magnetic field lines, _F), and boundary conditions at the BH horizon are known. A disc is necessary to confine the magnetic field that threads the hole's horizon and magnetic flux is advected into the hole by the infalling matter until B² / 8 P_disc. Once that condition is achieved any subsequent accretion would probably be by a slow "drip" process accompanied by magnetic reconnection, so no more flux is added to the BH. There should be a region between the BH horizon and infinity where particles are created, since some fall into the hole, while others are accelerated out to infinity. Physically, this could be accomplished by the photon-photon collisions mentioned above or by flares from the disc. The ratio _F / _BH determines the type of emergent wind. Optimal extraction of energy from the BH is conceivable if _F (1/5)_BH, for then there is near "impedance matching" between the magnetosphere load and the BH dynamo, and the power radiated is 64% of the conceivable maximum (which would occur if _F 1/2_BH, but is hard to arrange) (Phinney 1983). It also turns out that the maximum power can be extracted from a BH with a ~ 0.85, for while raising the spin of the hole increases the effective EMF, at very high values of BH angular momentum the field is excluded from the horizon because of the strong dragging of inertial frames (Phinney 1986).

The recently developed "membrane" technique, based upon the 3+1 split of spacetime into space + time, for treating BH physics provides the mathematical and conceptual framework which allows extensions of calculations such as the ones just discussed to be performed (Macdonald & Thorne 1982; Thorne 1986; Thorne et al. 1986). For example, using this approach it is surprisingly simple to demonstrate that the mass of the hole decreases due to both spindown and ohmic heating exactly at the rate at which energy is deposited in a resistive load between an assumed perfectly conducting disc and the BH; i.e., (Thorne 1986)

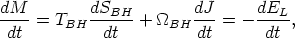
(20)

where T_BH and S_BH are the temperature and entropy of the BH given by

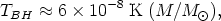
(21a)

and

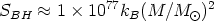
(21b)

and dE_L/dt = I² R_L, with I the current generated by this battery-like BH through the plasma of total resistance R_L. Although the application of this technique to specific cases through numerical simulation has begun (Macdonald 1984), much more remains to be done if sufficiently realistic models along these lines are to be produced.

The ability of magnetospheric models to produce and accelerate beams with relatively high ratios of kinetic power to photonic emission is a strong point and highly desirable for ordinary radio galaxies. While all explicit beam shapes are based upon extremely simplified assumptions, there is no reason not to expect that quite well collimated, relativistic jets can emerge, carried outward by the powerful Poynting fluxes. Hence this general approach must be considered a favourite explanation for the origin of jets at this stage, but the high degree of uncertainty involved in any application to date should be borne in mind.

2.3.2. Ion supported tori

As mentioned above, thick accretion discs supported by radiation pressure will always have L L_E, while many active galactic nuclei, particularly in radio galaxies, emit L << L_E in the optical and UV bands where the bulk of the disc radiation should emerge. However a geometrically thick disc, with the natural ability to launch and collimate beams, can radiate much less than L_E if it is supported by ions whose temperature is much higher than that of the electrons (Rees et al. 1982); see Fig. 3.

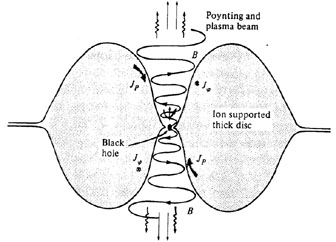
Figure 3. Very low accretion rates and strong magnetic fields can produce optically thin, but geometrically thick ion-supported discs that tap the black hole's rotational energy.

Such a two-temperature disc could be established in the inner regions of an accretion flow (where r/R_s < m_p / m_e) if the bulk motions connected with the infall are easily randomized and if the plasma spirals inward on a time scale shorter than its cooling time so that the energy of the ions is not shared with the electrons. Under these circumstances the ion temperature can lie close to the value expected from the virial theorem while the electron temperature would stabilize at a much lower value:

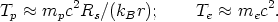
(22)

These ion-supported tori might exist if the densities are low enough and this translates into an upper limit on the accretion rate (Rees et al. 1982)

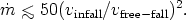
(23)

If collective effects are inefficient at coupling ions to electrons so that Coulomb collisions dominate the energy exchange, then this picture is viable, and extremely subcritical accretion can still produce bloated geometries.

Approximate models of such discs can be made with some additional assumptions. For example, if the ions are hot, but non-relativistic, then the effective specific heat ratio is ~ 5/3 and if ^* constant then r^-3/2 so the bulk of the mass of the torus is at large radii. The ions would be roughly isentropic in such a model and the pressure and temperature maxima would occur very close to the BH. The shapes would be very similar to those of radiation supported tori, with narrow funnels along the spin axis of the BH.

Because the accretion rate is very low the power emitted through viscous heating would also be very small, and the production of any powerful jets requires extracting part of the spin energy of the BH by means of magnetic fields, as discussed above. Let us now consider some specific results relevant to the context of ion supported tori. If B_pH is the poloidal field in the flux tube that intersects the hole's horizon, and a is the Kerr parameter, a small amount of matter flowing along that tube into the negative energy orbits inside the ergosphere of the BH can produce an external positive Poynting flux of luminosity (Rees et al. 1982)

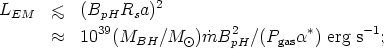
(24)

where P_gas is the maximum gas pressure in the torus. Typical values might be M_BH ~ 10⁸ M, ~ 10^-4, and ^* ~ 0.01 with P_gas B_pH², so powers of ~ 10⁴⁴ erg s^-1 are envisioned. The magnetic field would be predominantly toroidal and confined to the funnels, while large toroidal currents and return poloidal currents would flow in a thin surface layer of the ion supported disc. The Poynting flux would rapidly become infiltrated with a plasma and the domination of the toroidal fields would produce a self-collimated beam (e.g., Chan & Henriksen 1980; Blandford & Payne 1982).

Such an extremely efficient scenario fits both evolutionary (Blandford 1986) and "unified" models of AGN where M_BH, and the viewing angle to the beam, , determine the observed category of object (e.g. Blandford 1984), and this is indubitably a large part of its appeal. Early high accretion phases could produce standard thin or thick accretion discs that would be very bright optically and correspond to quasars or Seyferts. During this phase the SMBH would both grow in mass and spin up to a high value of a. But when the available supply of plasma dwindles then an ion supported torus could take over; spin energy could slowly be extracted from the SMBH. Now the energy output in relativistic, low density beams would far exceed c², but the optical emissivity would be very low: a typical strong radio galaxy could be produced.

However this particular picture requires that the magnetic field associated with the infalling matter must be very small, for otherwise the external fields would probably yield a very efficient outward transfer of both energy and angular momentum, thereby restricting L_EM to less than about c². While it is possible for this to be true, and it is also possible that the required minimal mechanical coupling between the beam and the torus be achieved, it is by no is means clear that this is likely. Yet another uncertain requirement of this model is that it demands that no collective plasma processes are efficient enough to couple the ions and electrons in the torus on a much shorter than a Coulombic interchange time scale.

While this model is definitely ingenious and has been very widely cited, its complexities and uncertainties undoubtedly explain why it has not been elaborated upon until very recently. Because the temperatures involved are so high, electron-positron pair production ought to be considered in conjunction with such discs and it turns out that its effect can be very important (Begelman et al. 1987; Tritz & Tsuruta 1989). Two basic mechanisms of pair production are possible: pair creation by photon produced by collisional processes in the thermal plasma will be important since such high temperatures are involved, but a nonthermal "cascade" initiated by photo-photon collisions in the presence of magnetic fields may dominate. Regardless of the assumed mechanism of pair production, it is likely that the large additional number of leptons in the innermost part of the flow produces many more collisions with the ions so that the Coulomb scatterings are more frequent and the ions' energy is quickly shared with the electrons. Begelman et al. (1987) argue that this strongly cooled inner part of the flow yields a small optically thick but geometrically thin disc that could couple to the two-temperature accretion flow further out if 0.1. If thermal pairs predominate, such a dual-type model appears to be explicitly unstable, with the inner annulus expanding outward since the photons it emits can cool the outer part of the flow. This modified model implies that abrupt transitions between types of flow with and without cool inner discs can occur even though change in the accretion rate are only small and continuous. Such a shift in the nature of the flow might provide the explanation for some types of sudden flares and spectral changes in AGN.

The combination of the above uncertainties, coupled with the possibility that instabilities similar to those discussed above for radiation supported thick accretion discs might afflict these ion supported tori, means that we cannot have real confidence in this entire class of model yet. However, its promise remains high and justifies intensive study.

2.3.3. Magnetized disc models

Another class of models assumes that magnetic fields are of extreme importance in the production of beams, but do no rely upon extracting energy from the BH. In these scenarios the accretion disc's fields are used to accelerate and collimate charged particles (Fig. 4).

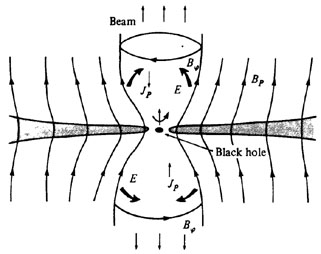
Figure 4. Magnetic fields can also dominate the energy extracted from a geometrically thin, optically thick disc.

An interesting dynamo mechanism which yields two steady collimated beams of ultrarelativistic protons can be produced if a disc is assumed to be both conductive and magnetized (Lovelace 1976). The key assumption is that the differential rotation in the inwardly spiralling matter tends to amplify the z-component of the field, and for simplicity it is assumed that B is non-vanishing only within the disc. Then a large potential between the inner (r_in) and outer (r_out) edges of the disc of

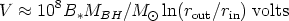
(25)

is generated, where B_* = max(B_z), is expected to be ~ 10³ gauss. A plasma capable of conducting a return current back to the disc is assumed to exist so that charge neutrality can be maintained in the disc. If B_z is anti-parallel to the angular momentum vector of the disc, then the potential on the disc implies that electric fields (v / c)B_z are produced; this greatly exceeds the gravitational attraction of protons to the disc, but is weak with respect to the poloidal magnetic field. In this case, a self-consistent space-charge limited flow of protons will yield a current, I cV (Lovelace 1976) off both faces so that the total power in the two beams is

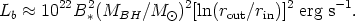
(26)

On the other hand, if the magnetic field and angular momentum vectors are parallel rather than anti-parallel, electrons rather than protons are preferentially stripped off the disc, but similar voltages and powers can be achieved (Lovelace et al. 1979). In this latter case, electromagnetic cascades should produce an overall neutral e⁺e^- beam, triggered by primary -rays. Although the voltages traversed are huge (~ 10²¹ V for reasonable parameters) the particles do not reach energies corresponding to those voltage drops because of Compton and synchrotron losses (especially for the electrons). Note that in this scenario, the energy of the BH is not extracted and the efficiency for mass to energy conversion is the same as for that in thin discs, i.e., 0.32. This type of neutral beam may be more stable than other beams (Lovelace et al. 1979), but there are several strong constraints on such beams.

It has been shown that an e⁺e^- beam is almost certainly very optically thick to scattering (and therefore cooling or annihilation) at the scale of 10¹⁵ cm if it is powerful enough to drive a strong double source (Rees 1984b). In particular, it is necessary that

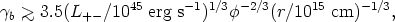
(27)

where _b is the bulk Lorentz factor of a lepton beam of power L_{+ -} and opening angle . The effective random Lorentz factor in such a beam is almost certainly reduced to ~ 1 through either synchrotron or Compton losses. The conclusion is that the bulk of the random motion must either be efficiently converted to ordered flow, or predominantly converted to a narrow beam of photons (of opening angle max[, _b^-1]), at least by the time the small distances of 10^-3 pc are reached. But lepton beams will also suffer severe Compton drag from the ambient radiation field, indicating that such high values of _b are hard to maintain over extended distances (Rees 1984b).

A different approach involves investigation of self-similar solutions to the perfect MHD equation

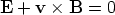
(28)

for flows driven from Keplerian discs (Blandford & Payne 1982). Several specialized assumptions allow analytic solutions to be obtained. For example, if the Alfvén speed ( B / ) scales with the Keplerian velocity and the specific angular momentum and energy fluxes scale with those for Keplerian discs, then the rate of mass loss per logarithmic radial interval is independent of radius. In this situation, r^-3/2, while B r^-5/4, and the sound speed, c_s r^-1/2, so the pressure is proportional to r^-5/2. These centrifugally driven winds exist if the poloidal component of the magnetic field makes an angle 60° with the disc's surface (Blandford & Payne 1982; Shibata & Uchida 1985). An interesting feature of these winds is that at large distances the toroidal field component becomes significant, and eventually collimates the outflow. These beams confine their power mainly to a central core, while the bulk of the angular momentum and flux are removed near the beam walls. Such a configuration would have a unique radio structure signature, but whether it would be observable has not been worked out. High resolution studies of relatively close sources, such as M87, are most likely to be useful in this regard if any such structure extends to the parts of the jet well outside the nucleus.

Somewhat related calculations have recently been performed within the framework of supermassive discs supported by rotation and magnetic fields (Camenzind 1986a, b; Kundt 1987).

Recently, a more elaborate treatment of MHD discs around BHs has been presented (Lovelace et al. 1986; Lovelace et al. 1987). Assuming a perfectly conducting disc and neglecting viscosity the MHD equations of motion and Maxwell's equations can be combined into one massive second-order non-linear partial differential equation of the Grad-Shafranov type (Lovelace et al. 1986). Within this framework a general family of thin magnetized discs around a Schwarzschild BH cannot have total magnetic energy greater than ~ 36% of their gravitational binding energy and sensible magnetic field configurations are expected to have major effects on the disc structure. The field tends to compress the disc vertically and since the magnetic force on the disc matter acts outward in the inner regions and inward in the outer regions of the disc, the azimuthal velocity of the disc matter in the inner part may be far less than the Keplerian value.

Generalizing the above model to viscous, resistive MHD thin discs leads to some very interesting results. A force-free plasma is again assumed to lie outside the disc, so the claim that this situation is not stable should be borne in mind (Phinney 1983, 1986); nonetheless, those claims are not overwhelmingly convincing, so that these new calculations are worth summarizing. Combining Ampere's Law and Ohm's law with Faraday's Law leads to the induction equation (Lovelace et al. 1987):

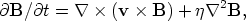
(29)

with = c² / (4 ), the magnetic diffusivity; is probably fairly large, being determined by macroscopic MHD instabilities. Solutions are found by breaking the flux function inside the disc, rA, with A the toroidal component of the vector potential, into odd and even functions of z. Magnetic stresses due to field-line "leakage" from the disc as well as radiative power-losses and unipolar induction effects can be incorporated into thin disc equations of vertical structure, angular momentum balance, and energy balance in a natural fashion. Then both and the toroidal magnetic field within the disc can be solved for in terms of Fourier expansions.

Outside of the disc, far field solutions of the "pulsar equation" can be found using a Green's function technique. One class of such solutions, which appears to be produced by sensible boundary conditions, are self-collimated electromagnetic beams. Because this collimation is due to the magnetic pinch effect, it does not depend on the existence of a narrow vortex. These electromagnetic beams are naturally relativistic and have radii smaller than the speed-of-light cylinder for the disc, in contrast to the non-relativistic MHD outflows mentioned above (Blandford & Payne 1982). Such beams carry axial and toroidal current densities as well as initially non-zero charge densities, but as they propagate outwards they will become charge neutralized before the current is neutralized.

It turns out that the emerging power is subject to a global consistency requirement which limits the fraction of the accretion power carried off by these beams. If is an odd function of z this fraction is very small, but if is an even function of z it appears that this fraction can approach unity. Lovelace et al. (1987) argue that quasars and other optically active AGN might correspond to cases where is odd and the vast bulk of the emission would be quasi-thermal radiation, while radio jet sources could be related to situations where is even and the bulk of the accretion energy is carried off by the electromagnetic beams. This approach is new and complex, yet, as always, somewhat oversimplified. The detailed properties of the emerging beams must be calculated and some attempts to compare them with observations must be made. Until that is done and the basic nature of the magnetosphere is clarified it will be too soon to pass judgement on this most intriguing possibility.