Each of the three new methods for the determination of masses of nebulae which have been described makes use of a different fundamental principle of physics. Thus, method iii is based on the virial theorem of classical mechanics; method iv takes advantage of the bending of light in gravitational fields; and method v is developed from considerations analogous to those which result in Boltzmann's principle in ordinary statistical mechanics. Applied simultaneously, these three methods promise to supplement one another and to make possible the execution of exacting tests to the results obtained.
Method iii can be applied advantageously only to clusters. Its application calls for the observation of radial velocities of cluster nebulae. The absolute dimensions of the cluster investigated also must be known.
Method iv involves the observation of gravitational lens effects. Measurements of deflecting angles combined with data on the absolute distance of the "lens nebula" from the observer suffice to determine the mass of the lens nebula. The chances for the successful application of this method grow rapidly with the size of the available telescopes. Since method iii gives only the average masses of cluster nebulae and method v furnishes only the ratios between the masses of different types of nebulae, much depends on whether or not a single image of a nebula, modified through the gravitational field of another nebula, can be found. A single good case of this kind would, so to speak, provide us with the fixed point of Archimedes in our attempt to explore the physical characteristics of nebulae.
Method v is the most powerful of all, since it enables us in principle
to find the masses of all types of nebulae, provided the absolute
mass of a single type of nebula is known or that we have some
independent way of finding a sufficiently accurate value of
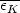. Method v
also results automatically in the knowledge of the statistical weight
functions f which govern the distribution of nebulae. The knowledge
of these functions is of interest for two reasons:
1. The weight functions derived from direct observations may be compared with those to be expected theoretically, for different "models" of the universe. Through such a comparison it should be possible to decide whether the universe as a whole is in thermodynamic equilibrium (12), (13) or is continually changing.
2. It will be of particular interest, as proposed previously, (14) to investigate the probability P of the occurrence of clusters of nebulae in our "immediate" extragalactic neighborhood, as well as at great distances. If the universe is, for instance, expanding, we should expect P to be different at different distances from the observer. The fact that a great cluster of nebulae, such as the Coma cluster, seems to represent a statistically stationary configuration suggests that a short time scale with 109 years as the characteristic age of the universe is hardly adequate. Considerably longer time intervals would seem to be necessary to insure the formation of a stationary distribution of nebulae in great clusters. A detailed analysis of the problem of the time scale, however, must be postponed until the distribution of nebulae in a greater number of clusters has been investigated.
CALIFORNIA INSTITUTE OF TECHNOLOGY
PASADENA, CALIFORNIA
June 1937
12 P. S. Epstein, Commentary on the Scientific Writing of J. W. Gibbs (New Haven: Yale University Press, 1936), 2, 104. Back.
13 F. Zwicky, Proc. Nat. Acad., 14, 592, 1928. Back.
14 F. Zwicky, Phys. Rev., 48, 802, 1935. Back.