© CAMBRIDGE UNIVERSITY PRESS 2000

13. ORBITS

The theory of orbits is an important ingredient in the study of the dynamics of galaxies. Because the relaxation times for the relevant processes are very long (see Chapter 7), much of the interest lies in the study of orbits in a mean field. What is learned from these studies applies beyond the case of single particles, for the evolution operator in a continuum description (either in a fluid or in a stellar dynamical description, see Chapter 8) can be essentially identified with the Hamiltonian that governs single particle orbits.

Galaxy disks are relatively "cool" systems, that is most star (or gas cloud) orbits are very close to being circular, so that a typical star (or gas cloud) velocity at a given location is very close to the average velocity of rotation of the disk. A proper description of a collection of orbiting particles should be given in terms of a distribution function (see Chapter 14). On the other hand, the physically intuitive properties of such cool disks can be easily traced back to the characteristics of quasi-circular orbits of individual particles, which will be outlined below in this Chapter. The deviations from circular orbits are called epicycles. To lowest order they correspond to a harmonic oscillator in the radial direction characterized by the epicyclic frequency . In cool disks the typical radial velocity of a star c is much smaller than the local average velocity u. Thus the epicycle is small, because the typical radial excursion c / is much smaller than r. Note that the typical restoring force associated with the radial oscillations (which is basically determined by the conservation of angular momentum) is c, which turns out to be of the order of the vertical force due to the self-gravity of the disk 2 G . This point will be further discussed in relation to the problem of density waves in Chapter 15.

The epicyclic motion is analogous to the Larmor oscillation of a charged particle in a magnetic field (see Fig. 13.1). The analogy is the basis for the development of common tools of investigation, as will be described at the end of this Chapter. These studies separate the orbit in two parts, the orbit of a guiding center, which reacts to perturbing forces perpendicular to the gyration axis in terms of drifts rather than accelerations, and the rapid oscillations (Larmor or epicyclic) around it. One useful concept of classical dynamics that has found wide applications in the description of the motion of charged particles in plasma physics is that of adiabatic invariant ⁽¹⁾. A well known example is that of the ratio of the energy associated with the Larmor oscillation and the cyclotron frequency. Under appropriate conditions, this quantity is approximately conserved when the particle moves in an inhomogeneous and/or time-dependent field, which is the key to a simple interpretation of a number of interesting phenomena, such as the trapping of particles in a magnetic mirror. This has a simple counterpart in the study of star orbits in a cool disk.

Figure 13.1. Decomposition of a quasi-circular orbit into circular and epicyclic motion (upper figures; after Bertin, G., Lin, C.C. 1996, Spiral Structure in Galaxies: A Density Wave Theory, MIT Press, Cambridge, MA, p. 70; © 1996 Massachusetts Institute of Technology). Sketch of a Larmor gyration of a charge moving in a magnetic field and the phenomenon of magnetic trapping in a mirror field (lower figures; these figures are taken from Schmidt, G. 1979, Physics of High Temperature Plasmas, 2nd ed., © Academic, New York, pp. 19, 22; 1979 Academic Press Inc.).

From the empirical point of view, the best chance we have for a direct measurement of the properties of individual stellar orbits in a galaxy disk is that provided by the solar neighborhood. On the other hand, the systematic motions occurring in the disk of our Galaxy are not easily derived from the observations, just because the Sun is part of such general flow. A classical study by Oort ⁽²⁾ managed to provide the empirical demonstration that our Galaxy is in a state of differential rotation, as proposed earlier by B. Lindblad. The basis for that study was the idea of expanding the average velocity field (flow field) in Taylor series around the location of the Sun, from which one could easily express the properties of the average motion relative to the Sun expected in the various directions in the sky, along the galactic plane, and at various distances from the Sun. In formulae

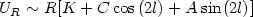(13.1)

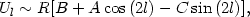(13.2)

where R and l denote distance from the Sun location and galactic longitude. For a generic flow field u, the four constants that result from the Taylor expansion can be written as:

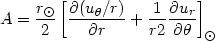(13.3)

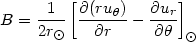(13.4)

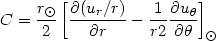(13.5)

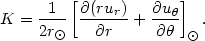(13.6)

Since the disk is cool, by observing the motion of groups of stars in various directions one can easily check that the flow is basically a pure differental rotation, i.e. one finds K 0 and C 0. Furthermore, the parameters A and B, called the Oort constants, obtained by fitting the data give the local properties of the galactic rotation curve. Note that for a pure differential rotation u_r = 0 and u ~ r (r), so that

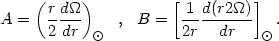(13.7)

These and other kinematical studies provide a rather detailed picture of the orbits of stars in the solar neighborhood ⁽³⁾, where it is found < < _z ( 26 km / (sec kpc) so that the rotation period is 240 Myr; based on the Oort limit for the local mass density, described in Chapter 14, the vertical period of oscillation is 70 Myr). The vertical frequency of oscillation about the galactic plane is thus the fastest.

¹ See Kulsrud, R.M. (1957), Phys. Rev., 106, 205; Kruskal, M. (1962), J. Math. Phys., 3, 806; Northrop, T.G. (1963), The Adiabatic Motion of Charged Particles, Interscience, New York Back.

² Oort, J.H. (1927), Bull. Astron. Inst. Netherlands, 3 (no.120), 275 Back.

³ The precise numbers are subject to several sources of uncertainties; see Kerr, F.J., Lynden-Bell, D. (1986), Mon. Not. Roy. Astr. Soc., 221, 1023 Back.