© CAMBRIDGE UNIVERSITY PRESS 2000

13.1. Action and angle variables

For the dynamics of disk galaxies the basic situation to be considered is that of a mean field potential that is stationary and axisymmetric around the z-axis. Note that such potential is very different from the Keplerian potential generated by a point mass located at r = 0. In the equatorial plane defined by z = 0, the calculation of orbits is reduced to a one-dimensional problem by introducing an effective potential

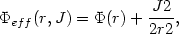(13.8)

so that the energy integral can be written as

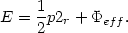(13.9)

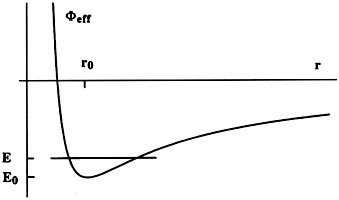Figure 13.2. Sketch of the effective potential for equatorial orbits in an axisymmetric field.

Thus the radial momentum (in our case this is identified with the radial velocity) can be expressed as a function of r and of the integrals of the motion E and J, with J the specific angular momentum. For a large class of potentials, the function _eff exhibits one minimum at r = r₀ (see Fig. 13.2), which identifies the radius of circular orbits with angular momentum J. If we take J > 0, and define

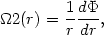(13.10)

the guiding center radius is related to the specific angular momentum by

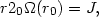(13.11)

which is generally one-to-one; in order for _eff to exhibit a minimum at r₀, the function J = J(r₀) defined by Eq. (11) must be monotonically increasing. Typically, for a given value of J bound orbits are associated with energies in the range E₀ < E < 0, with

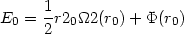(13.12)

the minimum energy which corresponds to the circular orbit. In the radial coordinate the motion is periodic and takes place between two turning points r_in(E, J) < r₀ < r_out(E, J). A radial action variable can thus be set

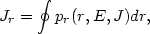(13.13)

with the property

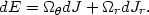(13.14)

Here the radial frequency is defined as _r = 2 / _r, with the bounce time given by

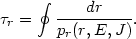(13.15)

In turn, the angular frequency is defined by

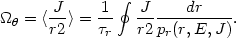(13.16)

Orbits are closed (in the inertial frame of reference) if the ratio between the two frequencies is rational.