© CAMBRIDGE UNIVERSITY PRESS 2000

13.4. Trapping at the Lagrangian points

We now consider a weakly non-axisymmetric potential of a form that is seen as stationary in a suitable rotating frame (rotating at angular velocity _p)

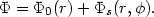(13.31)

For simplicity (and in view of a number of simple applications) we take

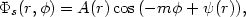(13.32)

with A, m > 0. The number m is integer. If the amplitude A(r) varies slowly and the phase (r) is instead rapidly varying, the potential _s may describe an m-armed spiral pattern with local pitch angle i determined by

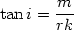(13.33)

where we have set k = d / dr. With respect to the azimuthal coordinate, at a given radial location the perturbing potential presents m maxima and m minima.

The perturbing potential _s is taken to be small, i.e. we consider the case when the non-axisymmetric forces are small:

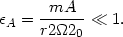(13.34)

Here ₀ is defined in terms of Eq. (10) based on ₀. We choose our frame of reference so that (r_co) = 0, with r_co the corotation radius.

Given the stationarity of _s, the Jacobi integral is conserved, while in the inertial frame the energy E and the angular momentum J vary along the orbits, with 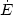= _p .

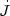In general the orbits are very complicated. However, in the rotating frame we may easily identify 2m points that are stationary, i.e. points where a particle released at rest can in principle stay in equilibrium. These are a generalization of the Lagrangian points that are known in the context of celestial mechanics. The equations of the motion show that these points occur at the stationary points of _s with respect to the azimuthal coordinate (m - ) = b, with b = 0, 1, 2...(2m - 1), so that the tangential force vanishes. The vanishing of the radial force requires that the following relation be satisfied:

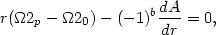(13.35)

where b is even or odd depending on whether _s is a maximum or a minimum (with respect to the azimuthal coordinate). Thus we see that the Lagrangian points occur in the vicinity of the corotation circle.

A curious behavior is found by checking the stability of these equilibrium points. For simplicity, one may focus on a case where A = constant, so that the stationary points are at r = r_co and at = b/m. Then, if we work out the linearized stability analysis for the motion in the neighborhood of r = r_co, = 0 (which under the above assumptions corresponds to a maximum of the perturbing potential along the corotation circle), we find the following relation for the eigen-frequencies of the normal modes of oscillations:

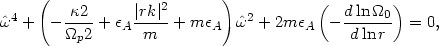(13.36)

where 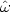= / _p, and all the r-dependent quantities are evaluated at the corotation circle. Thus we see that under the normal condition of monotonically decreasing (r) the point of maximum of the perturbing potential is stable. For small values of _A, one of the two frequencies derived from Eq. (36) corresponds to a modification of the (fast) radial epicyclic oscillation, while the new solution, which corresponds to the symmetry breaking and modifies the neutral displacements along the corotation circle at = 0, is a slow libration frequency, given by

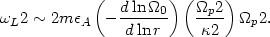(13.37)

Note the scaling 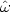_L ~ _A^1/2. In contrast, a similar analysis carried out at the perturbing potential minima at corotation would show that they are generally unstable.

The above study of the stationary points for a non-axisymmetric rigidly rotating potential is analogous to the classical restricted 3-body problem in celestial mechanics ⁽⁶⁾. A two-star or a star-planet (in circular orbit) configuration gives rise to five Lagrangian points. Two points are at 60 degrees with respect to the two masses on opposite sides on the plane of the orbit. The other three points are on the axis passing through the two masses. If the mass ratio is small (such as for the Sun-Jupiter case, for which the mass ratio is 10^-3), then all the five points are close to the "corotation circle", i.e. the circle of the orbit of the lighter mass. Then two of the three axial Lagrangian points are at a distance O(^1/3)r_co from the lighter mass, while the third is on the opposite side with respect to the heavier mass. If is sufficiently small (below a threshold value which is 0.04), then the two Lagrangian points off axis are stable, as is well known from the "trapping" of two separate families of asteroids in the solar system. The libration period scales as ^-1/2 also in this case.

Another application is found in the study of geostationary satellites, many of which are used for telecommunication purposes. In this case, the modification to the Earth's basically Keplerian potential occurs via a quadrupole term which fits in the description of Eq. (32) with = 0 and A(r) ~ 1/r3 (as can also be checked from the potential theory of the classical ellipsoids; see Chapter 10). This is because the mass distribution of the Earth is not perfectly axisymmetric. The rotating frame for which such non-axisymmetric perturbation is stationary is obviously the one that makes one turn in 24 hours. The weakness of the non-axisymmetric field is quantfied by the fact that the libration period about the two stable potential maxima is of 200 days.

The trapping of orbits close to a resonant circle is a rather general process which would be best described by use of action and angle variables ⁽⁷⁾. For example, at a Lindblad resonance for an m = 2 perturbation a trapping phenomenon occurs which refers to the major axis of the elliptical orbits that are closed in the axisymmetric case, but that are not closed because of the presence of _s. Thus for an m = 2 stationary perturbation the major axis slowly librates and is trapped around an appropriate direction, while it precesses away from a direction at 90 degrees from that.

13.4.1. Trapping of a charged particle on the top of a hill

The above discussion should be a reminder that the presence of rotation may bring in some counter-intuitive features in the properties of orbits. A simple problem in mechanics, where the presence of a magnetic field replaces the role of rotation, presents some analogies with the above case. It should also be stressed that the concept of stability investigated here refers to cases where no dissipation is present. From these examples it could also be appreciated why, in some circumstances, dissipation may have a destabilizing role ⁽⁸⁾ (see also Chapter 10).

Consider a charged particle (charge q, and mass m) constrained to move on a "hill" described by an axisymmetric surface z = z(r) in the presence of a constant vertical magnetic field B = B₀e_z and constant gravity g = - ge_z. Then in polar cylindrical coordinates the energy is

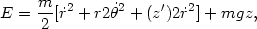(13.38)

which, because of the conservation of the canonical momentum associated with the axial symmetry:

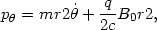(13.39)

can be written as

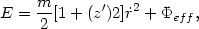(13.40)

with

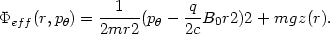(13.41)

Suppose

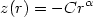(13.42)

with 1 < < 2 and C > 0. Then the orbit of the particle stays close to the top of the hill, which behaves as a stable equilibrium point even though it corresponds to the maximum of the potential energy.

⁶ Contopoulos, G. (1973), Astrophys. J., 181, 657 Back.

⁷ Lynden-Bell, D. (1973), in Dynamical Structure and Evolution of Stellar Systems, edited by L. Martinet and M. Mayor, Geneva Observatory Back.

⁸ M.D. Kruskal, as quoted in Coppi, B. (1966), in Non-Equilibrium Thermodynamics, Variational Techniques, and Stability, ed. by R.J. Donnelly, R. Herman, and I. Prigogine, Chicago University Press, Chicago, p. 259 Back.