© CAMBRIDGE UNIVERSITY PRESS 2000

13.5. Equations for the guiding centers

13.5.1. Larmor oscillations and drifts

We briefly recall the basic idea about the guiding center description of particle orbits ⁽⁹⁾ (see Fig. 13.6). Consider a charged particle (charge q, and mass m) moving in a constant magnetic field B in the presence of a constant force F

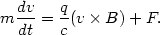(43)

Figure 13.6. Qualitative representation of the E × B drift (above) and magnetic gradient drift (below) for charged particles (from Krall, N.A., Trivelpiece, A.W. 1973, Principles of Plasma Physics, McGraw-Hill, New York, pp.612, 625; with kind permission of the authors).

One can separate the equations in the parallel and perpendicular directions (with respect to the magnetic field)

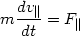(13.44)

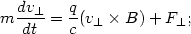(13.45)

then one separates the motion of the guiding center v₀ from the Larmor oscillation

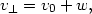(13.46)

so that

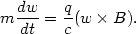(13.47)

The resulting guiding center motion is given by the relation

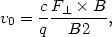(13.48)

from which it is evident that a perpendicular force produces a velocity and not an acceleration.

The more general, inhomogeneous and/or time-dependent, case where B and F are not constant can still be worked out with a similar strategy if the resulting drifts turn out to be slow and the basic gyration frequency is sufficiently fast. For example, a gradient in B can be absorbed in F in Eq. (45). Some effects, such as those due to the curvature of the field, may require some detailed analysis, which we do not need to record here ⁽¹⁰⁾. When the curvature is negligible, the parallel motion is basically reduced to solving the one-dimensional problem

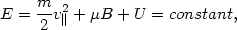(13.49)

where U is the potential associated with F_|| and µ = mv² / 2B is the adiabatic invariant associated with the Larmor gyration. Essentially the condition at the basis of this type of description is that the variations in the magnetic field encountered by the particle on its orbit be slow with respect to the relevant cyclotron frequency.

13.5.2. Star drifts and stellar hydrodynamics

Much like in the case of Larmor gyrations of charged particles in a magnetic field, the epicyclic theory can be extended to the case of weakly non-axisymmetric and weakly time-dependent fields. This tool allows one to gain a physical perception of the general properties of orbits without resorting to numerical surveys and well beyond the simple "small oscillations" that are considered in the standard stability analysis of the Lagrangian points, as we briefly gave in the previous section. The specific theory in the context of stellar dynamics ⁽¹¹⁾, formally developed for cool disks in the vicinity of the relevant corotation radius, is based on the generalization of the definitions of angular and epicyclic frequency as:

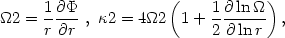(13.50)

where now is the sum of an axisymmetric potential and of a weakly non-axisymmetric and weakly time-dependent perturbation. Thus the guiding center orbits [r₀(t), ₀(t)] can be derived from an effective Jacobi integral

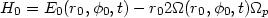(13.51)

where E₀ generalizes the concept of energy associated with the circular orbits Eq. (12):

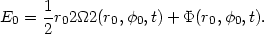(13.52)

The relevant equations of the motion are:

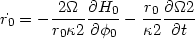(13.53)

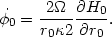(13.54)

The second term on the right-hand-side of Eq. (53) corresponds to the well known polarization drift of plasma physics. It should be stressed that in the presence of rotation the perturbation forces induce drift velocities in the motion of the guiding centers and not accelerations.

The complete properties of the orbits are then obtained by combining the information on the motion of the guiding centers with the fact that the adiabatic invariant µ is essentially constant:

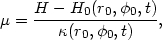(13.55)

where H is the star "Jacobi integral", which depends on the physical coordinates (r, ) and on the conjugate momenta.

When the perturbing potential is time-independent, the guiding center orbits are then simply obtained as contours of the function H₀(r₀, ₀). The Lagrangian points of the star orbit analysis described above are then recovered as stationary points for H₀; their stability properties are easily reconstructed by inspection of the relevant Hessian. If one takes as a perturbation a two-armed spiral potential of the form given in Eq. (32), one finds that the contours of constant H₀ identify two islands at corotation connected by a separatrix passing through the unstable potential minima (see Fig. 13.7). Outside the islands, moving away from corotation either inside or outside the corotation circle, the contours are in the form of distorted circles. This new shear flow configuration should be compared with the unperturbed shear flow. The trapped orbits at the stable Lagrangian points define some kind of "cat's eyes" ⁽¹²⁾. There is a clear analogy with the structure of magnetic islands that originate in plasma configurations via magnetic reconnection ⁽¹³⁾.

Figure 13.7. Vorticity islands marked by the guiding center orbits (in the corotating frame) in an axisymmetric disk in the presence of a two-armed rigidly rotating spiral field (from Berman, R., Mark, J.W-K. 1979, Astrophys. J., 231, 388). The structures created are reminiscent of magnetic islands that may result from reconnection in sheared magnetic configurations or cat's eyes that may originate from a shear flow. The lower frame shows full orbits, which can be seen as a result of the superposition of the slow libration of the guiding center and the rapid epicyclic oscillation (see also Contopoulos, G. 1973, Astrophys. J., 181, 657).

The concepts introduced in the present short Section find many applications in the context of magnetically confined plasmas, in particular in the description of trapped and circulating particles in toroidal plasma configurations ⁽¹⁴⁾. We will not pursue here these sources of analogies any further. In closing, we may just briefly refer to another development, which is conceptually very interesting. For a collisionless system it is possible to construct fluid equations from the moments of the collisionless Boltzmann equation (see Chapter 8). In the absence of collisions, a well known problem is how to close the fluid equations into a finite set, or, in more physical terms, how to define an appropriate equation of state. This question has found a solution in plasma physics in terms of the so-called double adiabatic theory ⁽¹⁵⁾, which makes use of the conservation of the adiabatic invariant to set a constraint equivalent to that of an equation of state. This leads to the justification of MHD-like equations for a collisionless plasma, with the peculiarity that pressure is to be considered anisotropic. It should be stressed that the closure is obtained under a set of assumptions that make the double adiabatic theory applicable only to a rather limited class of perturbations. Still the procedure is very interesting, especially from the physical point of view. A similar theory has been worked out for the context of the stellar dynamics of galaxy disks ⁽¹⁶⁾.

⁹ For example, see Schmidt, G. (1979), Physics of High Temperature Plasmas, 2nd edition, Academic Press, New York. Back.

¹⁰ See the book by Schmidt mentioned earlier; see also Krall, N.A., Trivelpiece, A.W. (1973), Principles of Plasma Physics, McGraw-Hill, New York Back.

¹¹ Berman, R.H. (1975), Ph. D. Thesis, Massachusetts Institute of Technology; Berman, R.H., Mark, J. W-K. (1977), Astrophys. J., 216, 257; Berman, R.H., Mark, J. W-K. (1979), Astrophys. J., 231, 388 Back.

¹² Kelvin, Lord (1880), Nature, 23, 45 Back.

¹³ See, e.g., White, R. (1983), Handbook of Plasma Physics, I, edited by A.A. Galeev, R.N. Sudan, North-Holland. Back.

¹⁴ Bertin, G., Coppi, B., Taroni, A. (1977), Astrophys. J., 218, 92 Back.

¹⁵ Chew, G.F., Goldberger, M.L., Low, F.E. (1956), Proc. R. Soc. London A, 236, 112 Back.

¹⁶ see Berman; Berman and Mark, op.cit. Back.