© CAMBRIDGE UNIVERSITY PRESS 2000

13.6. Exact orbits and the problem of self-consistency

Many interesting aspects of the theory of orbits relevant to the dynamics of spiral galaxies will not be treated in this book. It is the purpose of this Section to mention at least some key issues that are involved and then to comment especially on the subtle step of moving from the one-particle description to the collective behavior.

13.6.1. Three-dimensional orbits and polar ring galaxies

One important study addresses the properties of orbits outside the galactic plane. Here the basic reference case is that of an axisymmetric potential, with the equatorial plane defined by the galaxy disk. The field is in general significantly non-spherical, because of the presence of the disk, but also as a result of the flattening of the bulge-halo component. Thus, even for the quasi-planar case, we expect out-of-disk orbits to be subject to a "wobble", i.e. a precession. In general, a description of fully three-dimensional orbits requires the use of numerical integrations. Some well known methods of classical mechanics, such as the inspection of the relevant surfaces of section, help to point out the integrability properties of the assumed potential.

These investigations have found at least two important applications. In one study, which mostly addresses quasi-planar orbits, the relation between vertical and equatorial frequencies opens the way to a discussion of bending waves (see Chapter 19), much like the case of epicyclic oscillations properly introduces the analysis of density waves in the disk. Here one point should be stressed since it turns out to set a major difference between bending and density waves. The vertical restoring force on a star just off the galactic plane is due to two contributions. One is associated with the inhomogeneity of the disk and with the spheroidal bulge-halo component; even for a spherical field, at a radial location r on the disk the equatorial force is given by ²r, which translates, by projection, into a restoring force just off the plane F_z^{(1) 2} z. On the other hand the local disk self-gravity contributes (even in the absence of such a term; see also Chapter 14) by F_z⁽²⁾ 4 G z. The fact that _z in the solar neighborhood exceeds by a factor that is about 10^1/2 shows that at least in the middle of the optical disk, the local self-gravity term F_z⁽²⁾ should generally dominate. However, this strong restoring force does not count in the problem of bending waves, because these waves displace the disk as a whole, so that the local self-gravity of a patch of the disk does not act on itself when the patch is displaced from the equatorial plane. The subtlety involved in this point can be rephrased in the following way. With respect to the limit of zero-thickness, a bending wave is intrinsically non-linear. In any case it may be misleading to assign directly a term ²_z as the kinematical ingredient to the dispersion relation of bending waves. In contrast, there is no doubt that ² does place such a role for density waves, as the pioneering work of B. Lindblad first pointed out. These points will be discussed further in Chapter 19.

In a second application, the observation of kinematical properties of either individual objects (such as globular clusters) or of gaseous rings, significantly off the galactic plane, can be used to put a constraint on the underlying potential well of the galaxy ⁽¹⁷⁾. Indeed, there exists an interesting class of galaxies with prominent rings (the so-called polar ring galaxies; see Fig. 13.8), for which we have a chance of additional dynamical constraints beyond those provided by the standard rotation curve associated with the motion of the material in the disk. A general working hypothesis in many models of gaseous rings is that they are to be identified with closed orbits (for single particles) associated with the underlying potential. In reality, the dynamics of an observed ring is related to the "settling" of the gas into such an orbit ⁽¹⁸⁾, which may involve some non-trivial collective processes. Thus the related problem of diagnostics, i.e. the problem of reconstructing the underlying field from observed orbits, is generally marked by severe ambiguities. The astrophysical problem has an additional source of uncertainty, which is the fact that one generally has a very incomplete knowledge of the orbit under consideration.

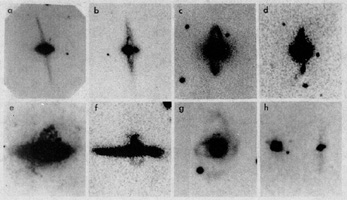Figure 13.8. Optical images of S0 galaxies with "polar rings": from left to right, starting on the top row UGC 7576, A 0136-0801, AM 2020-5050, ESO 603-G21, NGC 2685, ESO 199-IG12, ESO 474-G26, II Zw 73 (from Schweizer, F., Whitmore, B.C., Rubin, V.C. 1983, Astron. J., 88, 909). There are galaxies, such as NGC 3998 (see Knapp, G.R., van Driel, W., van Woerden, H. 1985, Astron. Astrophys., 142, 1), where the polar ring is observed only in HI.

13.6.2. Exact orbits in non-axisymmetric disks

Going back to the context of orbits in the galactic plane, we should mention that while the axisymmetric case is "trivial", the case of non-axisymmetric potentials opens a number of interesting possibilities even in the case where the perturbation is stationary in a suitable rotating frame. (A non-axisymmetric potential stationary in the inertial frame is probably of secondary interest, from the physical point of view.) In general, the orbits that violate the conditions for the guiding center description outlined earlier must be calculated numerically. Indeed large surveys of orbits have been performed, both in the presence of barred or ovally distorted potentials and in the presence of spiral fields ⁽¹⁹⁾. The orbits have thus been classified systematically ⁽²⁰⁾.

13.6.3. Orbital response and self-consistency

The simple interpretation of spiral arms as due to a collective crowding of orbits (as B. Lindblad initially suggested) has the major merit of focusing the discussion on the problem of quasi-stationary structures as due to waves ⁽²¹⁾, with remarkable attention to two-armed structures. On the other hand, such kinematical waves have the obvious shortcomings that they do not take into account the velocity dispersion of stars and, more importantly, that, when the spiral arms are set up, the gravitational field is no longer axisymmetric. We will study later, in Chapter 15, how those difficulties can be overcome. This point naturally introduces the problem of moving from a single particle description to the relevant collective behavior.

In practice, a quite severe problem arises immediately when we address the issue of non-axisymmetric fields. The study of orbits that we have outlined earlier, when thought in terms of a relatively large collection of orbits, is essentially an indication of the response of a specific component (such as a set of stars) to an imposed field. The trapping of stars at the Lagrangian points associated with the potential maxima is rather disconcerting, since the potential theory tells us that the potential maxima should roughly coincide with the density minima. Then the indication is that the orbits would act opposite to (out-of-phase with) the assumed spiral field, in other words that there is little chance that these non-axisymmetric fields would be naturally supported. This puzzling behavior can be partly softened by noting the general property that stars with guiding centers close to the separatrix, i.e. those that are barely trapped, spend a long time away from the trapping point, staying indeed close to the region where their presence would be needed to support the assumed field. This is just a suggestion, which shows that the problem of demonstrating how a field can be supported by the orbits that it imposes is non-trivial. On the other hand, as is recognized in a full analysis of density waves, the physical conditions for the establishment of density waves involve a number of issues (especially for non-barred spiral modes, in particular the dissipation in the gas) that go well beyond the single particle orbits.

In any case a systematic program to see whether stationary non-axisymmetric fields can receive adequate orbital support has been undertaken with a number of interesting results ⁽²²⁾. To some extent the issue that is addressed by these investigations is the same as the issue of finding triaxial self-consistent models by direct superposition of orbits, which has led to some notable results in the context of elliptical galaxies ⁽²³⁾.

¹⁷ See, e.g., Sackett, P.D., Rix, H.-W., Jarvis, B.J., Freeman, K.C. (1994), Astrophys. J., 436, 629 Back.

¹⁸ See, e.g., Christodoulou, D.M., Katz, N., Rix, H.-W., Habe, A. (1992), Astrophys. J., 395, 113 Back.

¹⁹ See, e.g., Contopoulos, G. (1973), Astrophys. J., 181, 657; Contopoulos, G., Papayannopoulos, T. (1980), Astron. Astrophys., 92, 33 Back.

²⁰ See Athanassoula, E., Bienaymé, O., Martinet, L., Pfenniger, D. (1983), Astron. Astrophys., 127, 349 Back.

²¹ A more detailed description of this important point can be found in Bertin, G., Lin, C.C. (1996), Spiral Structure in Galaxies: A Density Wave Theory, The MIT Press, Cambridge Back.

²² See Patsis, P.A., Hiotelis, N., Contopoulos, G., Grosbøl, P. (1994), Astron. Astrophys., 286, 46 and references therein; see also Lynden-Bell, D. (1979), Mon. Not. Roy. Astron. Soc., 187, 101 Back.

²³ Schwarzschild, M. (1979), Astrophys. J., 232, 236; Schwarzschild, M. (1982), Astrophys. J., 263, 599 Back.