© CAMBRIDGE UNIVERSITY PRESS 2000

22.1. Four approaches

It may be convenient to distinguish four different ways of working on the construction of stellar dynamical models. It should be noted that in some cases the differences are more in the perception than in the actual methods and a given model may be reached from different directions.

22.1.1. Search for interesting exact models

One simple way to proceed is to collect all possible self-consistent models. Usually here the emphasis is on the exactness or on the analytical simplicity of the models ⁽¹⁾. By producing a larger and larger set of potential galaxy models, one may hope to find some that are able to give a reasonable match to the observed profiles (see Chapter 4), others that are best suited for the numerical simulation of a specific dynamical mechanism (e.g., see Chapter 23), or models that are convenient to test special features, such as the structure of the line-of-sight velocity profiles (see section 22.1.3).

This "blind" search operates between two extremes. In one limit, spherical symmetry, with all the desired classical integrals of the motion readily available, appears to be a degenerate case. There is an infinite number of ways of specifying a distribution function and of constructing the related self-consistent model. Even here we may note that full self-consistency puts strong limitations to the set of solutions allowed by the Jeans theorem alone. In particular, much like for the classification of quantum states, the Jeans theorem would in principle allow any f = f (E, J², J_z). In practice, if we require that the spherical potential in E be generated by the distribution function itself, then we have to drop the use of J_z, i.e. we should work with f = f (E, J²) (in principle, an odd dependence on J_z would not break the symmetry of the mass distribution; on the other hand, the resulting internal streaming would correspond to the existence of a preferred axis, with no natural counterpart in the assumed symmetry of the problem). Still, within this framework we may construct models with a wide variety of density and pressure anisotropy profiles, and in many different ways we may match the main observed characteristics. Some notable models will be mentioned later in the context of distribution function priority models.

At the other extreme, the general triaxial case looks like an almost impossible task, at least from the analytical point of view. If we anticipate the possibility of three good integrals of the motion (in order to allow for a fully anisotropic pressure tensor), almost any combination f = f (E, I₂, I₃) is going to lead to a density distribution that is incompatible with the symmetry required for the existence of I₂, I₃. Stäckel potentials have three isolating integrals of the motion (see previous chapter) and offer a very wide choice of options (being specified in term of three free functions). They might thus be considered the natural environment for the construction of self-consistent triaxial models ⁽²⁾. Unfortunately, a discussion of Stäckel type density-potential pairs has shown the undesired feature that the associated density profile does not have sufficiently concentrated central regions (with the empirically suggested r^-2 density behavior). The application of a theorem ⁽³⁾, which guarantees the construction of a Stäckel potential with a desired set of axial ratios starting from a specified density profile along the z-axis, has shown that realistic density profiles can be obtained only at the cost of introducing a relatively massive disk ⁽⁴⁾. The issue of construction of triaxial models with central cusps is the focus of much work currently in progress ⁽⁵⁾. We should also recall that Stäckel potentials have been proved to be free of isophotal twisting ⁽⁶⁾, and so they are unable to reproduce the strongest empirical argument in favor of triaxiality.

Some more general triaxial models can be constructed by numerical superposition of stellar orbits in a density priority approach, in line with studies mentioned in section 21.4.

22.1.2. Density priority models

In the construction of models giving priority to the density distribution one specifies in advance the potential-density pair and then tries to invert the integral relation

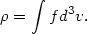(22.1)

One motivation at the basis of this point of view is very simple. The quantity that is best constrained by the observations, under the assumption of a constant mass-to-light ratio, is the projected density profile. If we add an assumption on the three-dimensional geometry of the system, we thus have an empirical determination of the volume density profile which appears on the l.h.s. of the above equation (further discussion of this point in connection with the empirical R^1/4 law is postponed to section 22.3.4 below). It is thus natural to ask, for various geometrical configurations whether a (positive definite) function of the integrals of the motion can be found compatible with the imposed density profile suggested by the observations. Furthermore we may ask whether, or under what conditions, such a solution is unique.

In the case of spherical symmetry, various options can be taken. Since the density profile depends only on the radial coordinate, the possibility of a unique inversion prescription is naturally expected when the distribution function (or the part of the function that is left free to vary) depends on one integral only. For example, if we take f = f (E), the solution is provided by an Abel inversion ⁽⁷⁾ (cf. Eq. (14.15) in Chapter 14)

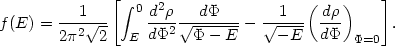(22.2)

In this inversion formula the density profile is assumed to be monotonic, so that the radial coordinate can be eliminated to give = (). The function f (E) resulting from the inversion should be checked to be positive definite. The model thus produced is characterized by isotropic pressure. Another possibility is to consider a dependence of f on a combination Q = Q(E, J²) specified in advance, thus producing anisotropic models according to some desired criteria. In this respect, the case where Q is a linear combination of E and J² has often been used especially to produce models with radially biased anisotropy profiles ⁽⁸⁾, with some difficulties appearing when tried for the construction of tangentially biased anisotropic models ⁽⁹⁾. Clearly, many other options can be considered and lead to several interesting models ⁽¹⁰⁾. Some separations with a rather intuitive basis can be adopted, focusing on a circularity function ⁽¹¹⁾ (which measures the distance from the relation J_circ(E), given for a few potentials in the previous chapter) or even on the epicyclic energy for the case where one aims at tangentially biased models ⁽¹²⁾.

For the case of axial symmetry a very elegant generalization of the Abel inversion has been devised ⁽¹³⁾ able to yield f (E, J²_z), for a given analytical axisymmetric potential; the method is based on a suitable contour integral in the complex plane. The most general triaxial case appears to require the use of direct numerical superposition of stellar orbits, as briefly indicated at the end of the previous chapter ⁽¹⁴⁾.

22.1.3. Deprojecting the data

We mentioned above that one motivation of the density priority approach is that of imposing the quantity that is best constrained by the observations. This viewpoint may be generalized in procedures where all the available observational constraints are imposed. In other words, models can be constructed basically by deprojection of the available photometric and spectroscopic profiles. In this respect, one aspect that has recently attracted much interest is the information contained in the line-of-sight velocity profiles ⁽¹⁵⁾; this is reminiscent of analogous interest in the 21 cm line profiles in radio observations of spiral galaxies ⁽¹⁶⁾.

In order to define the deprojection process, one may thus work with a mathematically convenient basis of distribution functions and try to determine empirically the combination leading to a best fit for all the available data. A simple class of these techniques involves the use of distributions that are polynomials ⁽¹⁷⁾ in E and J.

One may even bypass the explicit use of distribution functions and refer to numerical combinations of stellar orbits, with the additionl guidance of "cost functions" or "entropy functions" ⁽¹⁸⁾. An even more "abstract", non-parametric method has been proposed, with the important feature of ensuring that the derived distributions in phase space be smooth ⁽¹⁹⁾.

An alternative method resorts to the use of the moment "fluid" equations (see Chapter 8). The modeling can be carried through relatively easily in the axisymmetric case ⁽²⁰⁾. The moment equations can be simplified considerably if f = f (E, J_z) (without assuming any specific form for the underlying f), and become (using cylindrical coordinates R, z)

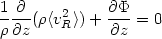(22.3)

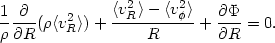(22.4)

The equations can be closed by making some assumption on the pressure anisotropy profile (often taken to be constant) and on the part of <v²> that is associated with systematic streaming motions. The photometric profiles taken at various position angles are fitted to provide information on the three dimensional structure of the galaxy and the density-potential pair thus inserted in the fluid equations gives the resulting kinematical profiles that are then compared with the spectroscopic data. In practical cases, the method may show whether reasonable fits can be provided with constant mass-to-light ratios and whether significant pressure anisotropies are involved. It is basically by means of these tools that it has been established ⁽²¹⁾ that most ellipticals are probably not too far from oblate systems with f = f (E, J_z). It is to be stressed that there is no guarantee that the solutions thus found admit a positive definite supporting distribution function. In addition, even when the solution selected by the data exists, it may require a rather artificial distribution of stellar orbits. In fact, we have already noted that descriptive methods of this kind tend to postpone the discussion of their physical justification.

As noted earlier in this chapter, one should be aware that the data points sample only limited spatial regions with good accuracy and that the inversion process is generally unstable, so that one may often be led to unrealistic or physically implausible distributions of stellar orbits.

22.1.4. Distribution function priority models

From the physical point of view, the methods mentioned so far remain unsatisfactory. For a collisionless stellar system all the physics is contained in the distribution function in phase space and most methods mentioned earlier leave the resulting distribution function "out of control" and without critical examination. To some extent it is as if, in making models of stellar structure, we first assigned the density profile inside the star and then we asked whether there is an equation of state able to justify the imposed density distribution, limiting the physical discussion to a study of uniqueness or to checking that the pressure profile is positive definite.

The fourth approach, i.e. the line of work better developed in this chapter, tries to overcome this criticism by attacking the problem at its roots. The idea is thus to proceed through a physically based choice of distribution function. This approach is thus predictive, in the sense that it tries to look for implications, both in terms of density profiles and of kinematical profiles, that should follow as a result of some physical scenarios. Current or future data may disprove the arguments put forward in this modeling process.

The main difficulty of this line of thinking is that the statistical mechanics of self-gravitating systems is poorly known and that there are very few empirical clues that we may take advantage of. Thus so far the most successful solutions are found for cases where the system is supposed to have relaxed significantly (see section 22.2) or for partially relaxed models of ellipticals where one exploits important clues offered by numerical simulations of collisionless collapse (see section 22.3). Note that in general the physical assumptions that offer a guidance in the choice of the relevant distribution function are unable to determine its form uniquely. This is also true for the choice of models described by Eq. (5) below, which represents only one available option within the physical scenario of isotropic quasi-Maxwellian truncated models.

The truncated "Maxwellian" distribution functions described in section 22.2 have found excellent applications to describe the structure and evolution of globular clusters, where indeed relaxation processes occur on a relatively fast timescale. The models define a very interesting one-parameter equilibrium sequence. In order to give a stronger physical justification to this and other models invoked to describe weakly collisional systems, the distribution functions have been compared directly to self-similar solutions of the Fokker-Planck equation ⁽²²⁾. The application of these models to elliptical galaxies is less justified but it is often considered.

For the description of collisionless stellar systems, such as elliptical galaxies, it would be important to produce, at least when the system is not too far from spherical symmetry, a model or classes of models under physical justification with the capability of realistic luminosity and kinematical profiles. Since one operates between the two extremes (spherical degeneracy and triaxial "impossibility") mentioned in section 22.1.1, the case of quasi-spherical symmetry is found to be simple enough to lead to some workable solutions, and, on the other hand, being away from strict spherical symmetry, to be able to teach us something beyond the spherical degenerate case. The models described in section 22.3 go in the desired direction, but so far they cannot be easily extended to cover cases where significant departures from spherical symmetry are involved.

Interesting attempts at constructing non-spherical models have been carried out, some focusing on the algorithm for the numerical solution of the Poisson equation ⁽²³⁾ and others on the more interesting aspect of including approximate integrals of the motion ⁽²⁴⁾. These attempts, giving priority to the distribution function, follow the most natural procedure of a physical approach, as is generally done in plasma physics ⁽²⁵⁾.

¹ See Dejonghe, H. (1986), Phys. Rep., 133, 217 Back.

² See discussion at the end of Chapter 21; Bishop, J.L. (1986), op. cit.; Statler, T.S. (1987), op. cit. Back.

³ Kuzmin, G.G. (1956), Astr. Zh., 33, 27 Back.

⁴ de Zeeuw, P.T., Peletier, R., Franx, M. (1986), Mon. Not. Roy. Astron. Soc., 221, 1001 Back.

⁵ See Merritt, D. (1997), Astrophys. J., 486, 102; Sridhar, S., Touma, J. (1997), Mon. Not. Roy. Astron. Soc., 292, 657 Back.

⁶ Franx, M. (1988), Mon. Not. Roy. Astron. Soc., 231, 285 Back.

⁷ Eddington, A.S. (1916), Mon. Not. Roy. Astron. Soc., 76, 572; see also Tricomi, F.G. (1985), Integral inversions, Dover, New York Back.

⁸ Osipkov, L.P. (1979), Pis'ma Astr. Zh., 5, 77; Merritt, D. (1985), Astron. J., 90, 1027; Merritt, D. (1985), Mon. Not. Roy. Astron. Soc., 214, 25p Back.

⁹ See Saha, P. (1991), Mon. Not. Roy. Astron. Soc., 248, 464 Back.

¹⁰ Hénon, M. (1973), Astron. Astrophys., 24, 229; Cuddeford, P. (1991), Mon. Not. Roy. Astron. Soc., 253, 414; Louis, P.D. (1993), Mon. Not. Roy. Astron. Soc., 261, 283 Back.

¹¹ Gerhard, O. (1991), Mon. Not. Roy. Astron. Soc., 250, 812 Back.

¹² In the context of tangentially biased models, Bertin, G., Leeuwin, F., Pegoraro, F., Rubini, F. (1997), Astron. Astrophys., 321, 703, compare a density priority model construction with a distribution function priority method Back.

¹³ Hunter, C., Qian, E. (1993), Mon. Not. Roy. Astron. Soc., 262, 401 Back.

¹⁴ See also Dejonghe, H., Laurent, D. (1990), Mon. Not. Roy. Astron. Soc., 252, 606 Back.

¹⁵ Franx, M., Illingworth, G. (1988), Astrophys. J. Letters, 327, L55; Bender, R. (1990), Astron. Astrophys., 229, 441; Rix, H.-W., White, S.D.M. (1992), Mon. Not. Roy. Astron. Soc., 254, 389; Gerhard, O. (1993), Mon. Not. Roy. Astron. Soc., 265, 213; van der Marel, R., Franx, M. (1993), Astrophys. J., 407, 525; Kuijken, K., Merrifield, M.R. (1993), Mon. Not. Roy. Astron. Soc., 264, 712. The results of Winsall, M.L., Freeman, K. (1993), Astron. Astrophys., 268, 443; Bender, R., Saglia, R.P., Gerhard, O. (1994), Mon. Not. Roy. Astron. Soc., 269, 785 on galaxies such as NGC 4472 argue for small departures from gaussian profiles and limited amounts of pressure anisotropy Back.

¹⁶ For example, see the discussion of radio emission from M 31 by van de Hulst, H.C., Raimond, E., van Woerden, H. (1957), Bull. Astron. Inst. Netherlands, 14, no. 480, 1 Back.

¹⁷ Dejonghe, H. (1989), Astrophys. J., 343, 113; Dejonghe , H., de Zeeuw, P.T. (1988), Astrophys. J., 333, 90; see also Merritt, D., Saha, P. (1993), Astrophys. J., 409, 75; Gerhard, O. (1991), Mon. Not. Roy. Astron. Soc., 250, 512; Saha, P. (1992), Mon. Not. Roy. Astron. Soc., 254, 132 Back.

¹⁸ Richstone, D.O., Tremaine, S. (1984), Astrophys. J., 286, 27; (1985), Astrophys. J., 296, 370 Back.

¹⁹ Merritt, D., Tremblay, B. (1994), Astron. J., 108, 514; Merritt, D. (1996), Astron. J., 112, 1085 Back.

²⁰ Binney, J.J., Davies, R.L., Illingworth, G.D. (1990), Astrophys. J., 361, 78; van der Marel, R.P., Binney, J.J., Davies, R.L. (1990), Mon. Not. Roy. Astron. Soc., 245, 582; van der Marel, R.P. (1991), Mon. Not. Roy. Astron. Soc., 253, 710 and many following papers Back.

²¹ See Franx, M., Illingworth, G.D., de Zeeuw, P.T. (1991), Astrophys. J., 383, 112 Back.

²² Spitzer, L., Härm, R. (1958), Astrophys. J., 127, 544; Hénon, M. (1961), Ann. d'Astrophys., 24, 369; King, I.R., (1965), Astrophys. J., 70, 376 Back.

²³ Prendergast, K.H., Tomer, E. (1970), Astron. J., 75, 674; Wilson, C.P. (1975), Astron. J., 80, 175 Back.

²⁴ Petrou, M. (1983), Mon. Not. Roy. Astron. Soc., 202, 1195 and 1209; Lupton, R.H., Gunn, J. F. (1987), Astron. J., 93, 1106 Back.

²⁵ Harris, E.G. (1962), Nuovo Cim., XXIII, 115; see section 9.1 in Part two Back.