© CAMBRIDGE UNIVERSITY PRESS 2000

Problems

1. Without addressing the issues involved in the solution of the self-consistent problem, consider simple analytical forms of distribution functions f (E, J2) able to display either a tangentially biased or a radially biased pressure tensor (note that the same distribution function can have anisotropy of the two kinds at different radii, but such an example is less easy to find). For cases where the pressure anisotropy is strong (i.e., for cases where either in the radial or in the tangential directions the system can be considered to be cold), describe the qualitative properties of radial and of tangential cuts of the distribution function in velocity space (obtained by taking either v = 0, v = 0 or v_r = 0, v = 0). What is a reasonable expectation for the associated velocity profiles projected along the line-of-sight in the two cases, if one uses the above models to match the observed line profiles of a spherical stellar system?
2. For an assigned potential (r), write the expression of a distribution function f (E, J2) for a system populated only by circular orbits. What is the corresponding function F(r, v_r, v) referred to the standard coordinates of spherical geometry?
3. For an anisotropic spherically symmetric stellar system without internal streaming motions, show that the hydrostatic equilibrium condition can be written as

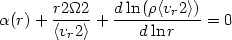   with the same notation used in the main text.

4. Consider a modification of a spherical distribution function f (E, J2) [1 + g(J_z)]f (E, J2) by a term that is odd in J_z, such as g(J_z) J_z / (J₀² + J_z²)^1/2, with J₀² a constant, so that the final function is positive definite. If the initial distribution corresponds to a fully self-consistent model, is this true also for the new function? Since the transformation leaves the even moments unaltered, is it true that the velocity dispersion profiles remain unchanged?
5. Consider the integration over velocity space of an isotropic function; how can the integral be transformed into an integral in dE? Suppose now the function to be integrated is anisotropic, but within the overall spherical symmetry (so that v and v are equivalent); how can the integral be transformed into an integral in dEdJ? What is the Jacobian of the transformation d3vd3x into dEdJdr appropriate for the case of spherical symmetry? In this last case, if the integrand does not depend on r explicitly, what is the result of a first integration in the radial coordinate?
6. Show that the quantity p_rr(, r) = v2_rfd3v, based on a distribution function f (E, J2) associated with a spherical potential (r), is related to density and to pressure anisotropy by simple differentiation

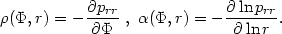   Note that in the isotropic case p_rr thus depends on r only implicitly through . Note also that the two relations lead to the correct hydrostatic equilibrium condition (see third problem for this Chapter).

7. For a purely isotropic distribution f = A(- E) exp(-aE), with a, A positive constants (f = 0 for E > 0), what is the value of compatible with a density distribution decaying as r^-4 at large radii?
8. Consider a stellar system, such as a globular cluster, to be initially characterized by energy E, mass M, and truncation radius r_t. Suppose that, as a result of some evolutionary processes (internal evaporation, disk-shocking, etc.), the stellar system changes energy by a small amount E, its mass by a small amount M, while changing r_t under the usual condition that r_t is determined by tidal interaction with the host galaxy (and under the assumption that, while the energy and mass have changed, the location of the stellar system inside the host galaxy can be considered to be practically unchanged). If initial and final states are well fitted by a King model, formulate and discuss a procedure to determine the parameter transformation (a, A, C) (a', A', C') induced by the combined effect of E and M.
9. Using the simple analytical model of section 22.3.4, check that for a spherical system conforming to the R^1/4 law one expects r_M 1.3R_e between volume and projected half-mass radii.
10. A one component f model with = 12 and mass-to-light ratio M / L_B = 6, fitting a galaxy characterized by absolute blue magnitude B = -20.7, effective radius R_e = 5 kpc, and observed central velocity dispersion 250 km/sec, is taken to be strictly correct and applicable all the way down to the center. What would be the expected core radius? What would be an estimate for the central relaxation time in this system? (Hint: The solution requires an investigation of the properties of the f models for high at r 0, with the scales set by the available data. One way to set the scales is to recall that R_e (a/c)^1/2 (to be more precise, a numerical study gives, for high- models, (a/c)^1/2 0.85r_M and it is known that for a model close to the R^1/4 law the relation r_M 1.3R_e holds), that the one-dimensional velocity dispersion at the center is (1 / a)^1/2, and that for high- models 18. Once the scales are set, a discussion of the density behavior in the vicinity of r = 0, as carried out in section 22.2.1 for the King models, quickly leads to the desired answers.)
11. Consider a cool homogeneous sphere characterized by total energy E_tot, mass M, and initial virial ratio (2K / | W|)_in = u << 1. As a result of collisionless collapse, suppose that a quasi-equilibrium is reached, well represented by an f model (with the same values of energy and mass). In this final configuration, the maximum phase space density should not exceed its maximum initial value. Find a relation between initial virial ratio (u) and final value () of the dimensionless central potential. (Hint: Make use of dimensional analysis and of the fact that the global properties of the "high-" models are basically -independent; more precisely, we may recall that a numerical study gives 18, q = | W| r_M / GM² 1/2, a| W| / M 3/4, and (a/c)^1/2 0.85r_M. A comparison between initial and final virialized states gives the relation (r_M / R) 5/12 between final half-mass radius and radius R of the initial homogeneous sphere. The constraint on maximum phase space density gives the maximum depth of the central potential well that can be formed by collisionless collapse, as _max^3/2 exp(_max) 2[u(1 - u/2)]^-3/2. For a related discussion, see Londrillo, P., Messina, A., Stiavelli, M. (1991), cited in Chapter 23.)
12. What is the relation between central dynamical time scale [G(0)]^-1/2 and global crossing time t_cr = GM^5/2 / | 2E_tot|^3/2 for high- f models?