© CAMBRIDGE UNIVERSITY PRESS 2000

Problems

1. For a disk with a perfectly flat rotation curve, V = const., let corotation be at r = r_co. Recall that the Inner Lindblad Resonance and Outer Lindblad Resonance locations are defined by the conditions m[(r_co) - ] / = -1 and +1. Where are ILR and OLR located for m = 2? What happens for m = 1 and for m = 3? Compare with the case of a Keplerian rotation curve.
2. Following the epicyclic expansion procedure outlined in section 13.2 prove that indeed the quantity A₂ has the expression recorded in Eq.(13.28).
3. Define the orbit (r_*(), _*()) along the "characteristics" (cf. Chapter 11) in an axisymmetric potential, with the conditions r_*(± _e) = r, _*(± _e) = ± _e. Here the quantities 2_e = _r and 2_e are functions of E and J and denote the radial period of oscillation of the stars in the equilibrium potential and the azimuthal angle traversed in such a period. Prove that, to two orders in the epicyclic expansion for the radial coordinate and to one order for the azimuthal coordinate, one can write

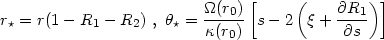   with s = (r₀) , _e = (r₀) / (r₀), _e = / (r₀), and

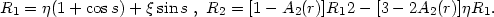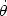   Here = a sins₀ and = a coss₀ are dimensionless radial and azimuthal epicyclic velocities associated with the orbit at = _e (cf. Eq.(13.20) and Eq.(13.22)). From the identity r₀² (r₀) = r_*² _* at = _e, check also that, to first order, r₀ = r(1 - ). (Hint: replace the r and variables in Eqs.(13.22)-(13.25) by r_*() and _*(), integrate the equations, and then impose the desired "boundary conditions". This is one key step towards the integration along the unperturbed characteristics of the stellar dynamical equations leading to the dispersion relation for tightly wound density waves; see Chapter 15 and the article by Shu, F.H. (1970) cited there.)

4. Consider the problem of the stability of geostationary satellites, on the equatorial plane, in view of the presence of a small departure from axisymmetry of the Earth's mass distribution and compare this problem to that of the trapping of star orbits at corotation in the presence of a rigidly rotating two-armed spiral field.
5. For the classical restricted 3-body problem, with = m / M << 1, find the approximate location of the two Lagrangian points close to m (note the singular character of the perturbation analysis involved in the identification of the distance from the smaller mass, O(^1/3) r_co; see section 8.5 for comments on singular perturbations).
6. For a system of two stars of equal mass orbiting around each other at a fixed distance, find the location of the associated five Lagrangian points and discuss the linear stability of orbits in their vicinity (in the framework of the restricted 3-body problem).