The classical way to use clusters to constraint the average matter density in to try to obtain a direct measurement of the local density. This is the principle of M/L test. Because the matter content of the universe is essentially in a dark form, we do not have direct measurement of the mass content even at the local level. This is the reason why in practice we rely on a two-steps procedure: first the average luminosity density of the universe is estimated from galaxy samples, this quantity is now relatively well known thanks to the large redshift surveys like the SLOAN or the 2dF (although difference of the order of 50% might still exist); the second ingredient is the value of the M/L ratio obtained from data on clusters (total luminosity and mass estimations). There might be a factor of two of uncertainty in this quantity. For instance Roussel et al. (2000) found that the average M/L could be as large as 750h when the mass-temperature relation for clusters is normalized from numerical simulations of Bryan and Norman (1998), while values twice smaller are currently obtained by other technics. The basic principle for estimating the average density of the Universe is then to write:
 |
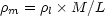(4) |
However, it should be realized that the volume occupied by clusters is a tiny fraction of the total volume of universe, of the order of 10-5. The application of the M/L relies therefore on an extrapolation over 105 in volume!
 |
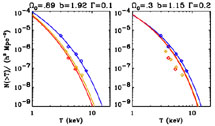Figure 4. These plots illustrate the power
of the cosmological test of the evolution of the abundance of X-ray
clusters: the TDF (temperature distribution function) has been
normalized to present day abundance (blue - dark grey - lines). The
abundance of local clusters is given by the blue (dark grey) symbols
(Blanchard et al.,
2000).
Present abundance allows one to set the normalization and the slope of the
spectrum of primordial fluctuations on clusters scale
(which is |
m
dependant). The
evolution with redshift is much
faster in a high matter density universe (left panel,