4.4. Abundance Gradient Variations

Another commonly-noted correlation is illustrated in the top panel of Figure 11: the steepness of abundance gradients (expressed in dex/kpc) decreases with galaxy luminosity. However, more luminous galaxies have larger disk scale lengths, and so if one looks at the gradient per disk scale length (Figure 11, bottom panel), the correlation goes away. Interestingly, when one considers the errors in the computed gradients (25% is a typical uncertainty), then the scatter in measured gradient slopes may be consistent with purely observational scatter. Combes (1998) has suggested that a "universal" gradient slope per unit disk scale length may be explained by so-called "viscous disk" models (Lin & Pringle 1987); if the timescale for viscous transport of angular momentum is comparable to the star formation timescale (with the two timescales connected through the gravitational instability perhaps), such models naturally produce an exponential stellar disk. Chemical evolution models invoking viscous transfer have been able to produce abundance gradients (Clarke 1989; Tsujimoto et al. 1995), but it is not yet clear from the few models examined that they can yield very similar abundance gradients per unit disk scale length for a wide variety of spiral disks. This is something that deserves further study.

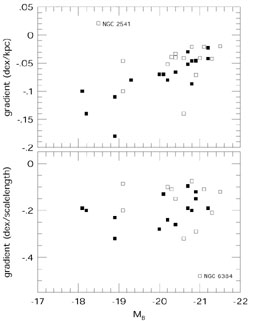Figure 11. The correlation of abundance gradient vs. MB, from Garnett et al. (1997a). The upper panel shows abundance gradients per kpc, while the lower panel shows gradients per unit disk scale length.

Another interesting possibility is presented by Prantzos & Boissier (2000). They constructed a sequence of chemical evolution models for disk galaxies by scaling the mass distribution (total mass, scale length) according to the scaling relations for cold dark matter halos of Mo, Mao & White (1998), in which the disk mass profile can be expressed using only two parameters: the maximum circular velocity (which corresponds to the halo mass) and the spin parameter (which corresponds to the angular momentum). A key assumption is that the scaled galaxies settle into exponential disks. Prantzos & Boissier computed models for galaxies under these assumptions, calibrated by reproducing measurements for the Milky Way. The basic results are illustrated in their Figure 4, reproduced here in Figure 12. The top panel plots the slope of the composition gradients in units of physical length (kiloparsecs) vs. M_B, the middle panel plots the gradients per unit disk scale length, while the bottom panel plots the gradient over the photometric radius R₂₅. In each case the model gradients are in good agreement on average with observed gradients, although the gradients per unit scale length and R₂₅ are perhaps a bit steeper than observed. If this analysis holds up it would be quite remarkable, as it would have been difficult to imagine that the present-day ISM composition could be related to the initial properties of the disks in the distant past. This may reflect the assumption that the baryons start out with exponential mass distributions. Prantzos & Boissier (2000) predict that there should be a small spread in observed gradients per kiloparsec in massive spirals and a large spread in small spirals, such that small spirals with large angular momentum should have shallower gradients (larger scale lengths) than those with lower angular momentum.

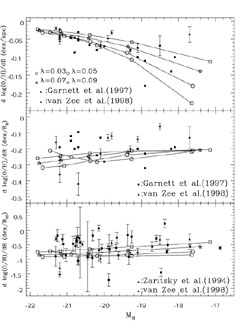Figure 12. Comparison of generalized chemical evolution models from Prantzos & Boissier (2000) with observed composition gradients for spiral galaxies. Top: O/H gradient in dex/kpc vs. MB. Middle: O/H gradient in dex per unit disk scale length vs. MB. Bottom: O/H gradient over the photometric radius R25 vs. MB. The curves show the model relations for constant for = 0.03, 0.05, 0.07, and 0.09.