The expansion of the Universe provides astronomers with the benefit that recession velocities can be translated into radial distances. It also presents the challenge that sources observed at different redshifts are sampled, by any particular instrument, at different rest-frame frequencies. The transformations between observed and rest-frame broad-band photometric measurements involve terms known as "K corrections" (Humason, Mayall, & Sandage 1956; Oke & Sandage 1968).
Here we define the K correction and give equations for its calculation, with the goals of explanation, clarification, and standardization of terminology.
In what follows, we consider a source observed at redshift z,
meaning that a photon observed to have frequency
0 was emitted
by the source at frequency
e with
 |
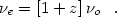(1) |
The apparent flux of the source is imagined to be measured through a finite observed-frame bandpass R and the intrinsic luminosity is imagined to be measured through a finite emitted-frame bandpass Q. The K correction is used in relating these two quantites.
Technically, the K correction described here includes a slight generalization from the original conception: The observed and emitted-frame bandpasses are permitted to have arbitrarily different shapes and positions in frequency space (as they are in, e.g., Kim et al. 1996) In addition, the equations below permit the different bandpasses to be calibrated to different standard sources.