2. EQUATIONS

Consider a source observed to have apparent magnitude m_R when observed through photometric bandpass R, for which one wishes to know its absolute magnitude M_Q in emitted-frame bandpass Q. The K correction K_QR for this source is defined by

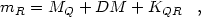(2)

where DM is the distance modulus, defined by

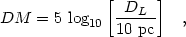(3)

where D_L is the luminosity distance (e.g. Hogg 1999) and 1 pc = 3.086 × 10¹⁶ m.

The apparent magnitude m_R of the source is related to its spectral density of flux f() (energy per unit time per unit area per unit frequency) by

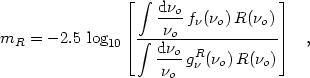(4)

where the integrals are over the observed frequencies ₀; g^R() is the spectral density of flux for the zero-magnitude or "standard" source, which, for Vega-relative magnitudes, is Vega (or perhaps a weighted sum of a certain set of A0 stars), and, for AB magnitudes (Oke & Gunn 1983), is a hypothetical constant source with gAB() = 3631 Jy (where 1 Jy = 10^-26 W m^-2 Hz^-1 = 10^-23 erg cm^-2 s^-1 Hz^-1) at all frequencies ; and R() describes the bandpass, as follows:

The value of R() at each freqency is the mean contribution of a photon of frequency to the output signal from the detector. If the detector is a photon counter, like a CCD, then R() is just the probability that a photon of frequency ₀ gets counted. If the detector is a bolometer or calorimeter, then R() is the energy deposition h per photon times the fraction of photons of energy that get absorbed into the detector. If R() has been properly computed, there is no need to write different integrals for photon counters and bolometers. Note that there is an implicit assumption here that detector nonlinearities have been corrected.

The absolute magnitude M_Q is defined to be the apparent magnitude that the source would have if it were 10 pc away, at rest (i.e., not redshifted), and compact. It is related to the spectral density of the luminosity L() (energy per unit time per unit frequency) of the source by

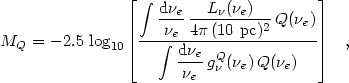(5)

where the integrals are over emitted (i.e., rest-frame) frequencies _e, D_L is the luminosity distance, and Q() is the equivalent of R() but for the bandpass Q. As mentioned above, this does not require Q = R, so this will lead to, technically, a generalization of the K correction. In addition, since the Q and R bands can be zero-pointed to different standard sources (e.g., if R is Vega-relative and Q is AB), it is not necessary that g^Q = g^R.

If the source is at redshift z, then its luminosity is related to its flux by

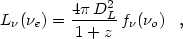(6)

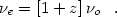(7)

The factor of (1 + z) in the luminosity expression (6) accounts for the fact that the flux and luminosity are not bolometric but densities per unit freqency. The factor would appear in the numerator if the expression related flux and luminosity densities per unit wavelength.

Equation (2) holds if the K correction K_QR is

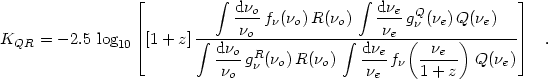(8)

Equation (8) can be taken to be an operational definition, therefore, of the K correction, from observations through bandpass R of a source whose absolute magnitude M_Q through bandpass Q is desired. Note that if the R and Q have different zero-point definitions, the g^R(_e) in the numerator will be a different function from the g^Q(₀) in the denominator.

In equation (8), the K correction was defined in terms of the apparent flux f() in the observed frame. This is the direct observable. Most past discussions of the K correction (e.g. Oke & Sandage 1968; Kim et al. 1996) write equations for the K correction in terms of either the flux or luminosity in the emitted frame. Transformation from observed-frame flux f(₀) to emitted-frame luminosity L(_e) gives

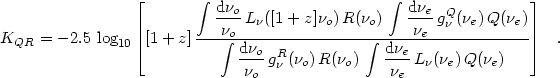(9)

In the above, all calculations were performed in frequency units. In wavelength units, the spectral density of flux f() per unit frequency is replaced with the spectral density of flux f() per unit wavelength using

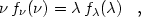(10)

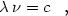(11)

where c is the speed of light. The K correction becomes

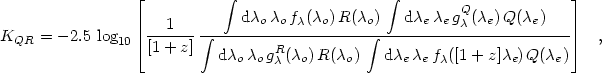(12)

where, again, R() is defined to be the mean contribution to the detector signal in the R bandpass for a photon of wavelength and Q() is defined similarly. Note that the hypothetical standard source for the AB magnitude system, with gAB() constant, has gAB() not constant but rather gAB() = c ^-2 gAB().

Again, transformation from observed-frame flux f(_o) to emitted-frame luminosity L(_e) gives

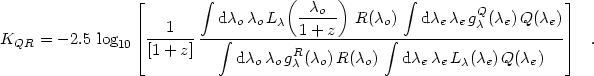(13)

Equation (13) becomes identical to the equation for K in Oke & Sandage (1968) if it is assumed that Q = R, that g^Q = g^R, that the variables ₀, F(), and S_i() in Oke & Sandage (1968) are set to

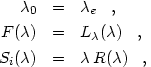(14)

and that the integrand is used differently in each of the two integrals. Similar transformations make the equations here consistent with those of Kim et al. (1996), although they distinguish between the classical K correction and one computed for photon counting devices (an unnecessary distinction); their most similar equation is that given for K_xy^counts.