2. GRAVITATIONAL WAVES AND CMB POLARIZATION

One the most intriguing avenues toward further tests of inflation is the gravitational-wave background. In addition to predicting a flat Universe with adiabatic perturbations, inflation also predicts the existence of a stochastic gravitational-wave background with a nearly-scale-invariant spectrum [Abbott & Wise 1984]. The amplitude of this inflationary gravitational-wave background (IGW) is fixed entirely by the vacuum-energy density during inflation, which is proportional to the fourth power of the energy scale E_infl of the new physics responsible for inflation.

Gravitational waves, like primordial density perturbations, produce linear polarization in the CMB. However, the polarization patterns from the two differ. This can be quantified with a harmonic decomposition of the polarization field. The linear-polarization state of the CMB in a direction 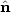can be described by a symmetric trace-free 2 × 2 tensor,

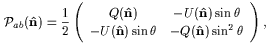(1)

where the subscripts ab are tensor indices, and Q(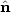) and U(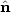) are the Stokes parameters. Just as the temperature map can be expanded in terms of spherical harmonics, the polarization tensor can be expanded [Kamionkowski et al. 1997a, Kamionkowski et al. 1997b, Seljak & Zaldarriaga 1997, Zaldarriaga & Seljak 1997],

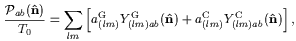(2)

in terms of tensor spherical harmonics, Y_(lm)ab^G and Y_(lm)ab^C. It is well known that a vector field can be decomposed into a curl and a curl-free (gradient) part. Similarly, a 2 × 2 symmetric traceless tensor field can be decomposed into a tensor analogue of a curl and a gradient part; the Y_(lm)ab^G and Y_(lm)ab^C form a complete orthonormal basis for the "gradient" (i.e., curl-free) and "curl" components of the tensor field, respectively. The mode amplitudes in Eq. (2) are given by

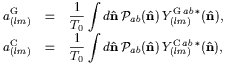(3)

which can be derived from the orthonormality properties of these tensor harmonics [Kamionkowski et al. 1997b]. Thus, given a polarization map _ab(), the G and C components can be isolated by first carrying out the transformations in Eq. (3) to the a^G_(lm) and a^C_(lm), and then summing over the first term on the right-hand side of Eq. (2) to get the G component and over the second term to get the C component. The two-point statistics of the combined temperature/polarization (T/P) map are specified completely by the six power spectra C^XX' for X, X^' = {T, G, C}, but parity invariance demands that C^TC = C^GC = 0. Therefore, the statistics of the CMB temperature-polarization map are completely specified by the four sets of moments: C^TT, C^TG, C^GG, and C^CC.

Both density perturbations and gravitational waves will produce a gradient component in the polarization. However, to linear order in small perturbations, only gravitational waves will produce a curl component [Kamionkowski et al. 1997a, Seljak & Zaldarriaga 1997]. The curl component thus provides a model-independent probe of the gravitational-wave background.

In Kamionkowski & Kosowski (1998) and Jaffe et al. (2000), we studied the smallest IGW amplitude that can be detected by CMB experiments parameterized by a fraction of sky covered, the instrumental sensitivity (parameterized by a noise-equivalent temperature s), and an angular resolution. We found that the sensitivity to IGWs was maximized with a survey that covers roughly a 5° × 5° patch of the sky (as indicated by the solid curve in Fig. 1) and with an angular resolution better than roughly 1°. The smallest detectable energy scale of inflation is then E_infl = 5 × 10¹⁵(s/25 µK sec^1/2)^1/2 GeV. For reference, the instrumental sensitivity for MAP is O(100µK sec^1/2) and for the Planck satellite O(20 µK sec^1/2).

Figure 1. Minimum inflaton potential observable at 1 as a function of survey width for a one-year experiment. The left panel shows an experiment with NET s = 25 µK sec1/2. The solid curve shows results assuming no CS while the dashed curve shows results including the effects of an unsubtracted CS; we take FWHM = 5' in these two cases. The dotted curves assume the CS is subtracted with FWHM = 10' (upper curve) and 5' (lower curve). Since the dotted curves are close to the dashed curve, it shows that these higher-order correlations will not be significantly useful in reconstructing the primordial curl for an experiment similar to Planck's sensitivity and resolution. The right panel shows results for hypothetical improved experiments. The dotted curves shows results with CS subtracted and assuming s = 1 µK sec1/2, FWHM = 5', 2', and 1' (from top to bottom). The solid curve assumes FWHM = 1' and s = 1 µK sec1/2, and no CS, while the dashed curve treats CS as an additional noise. The long-dash curve assumes CS subtraction with no instrumental noise (s = 0). From KesCooKam02.

However, since then, it has been pointed out that cosmic shear (CS), gravitational lensing of the CMB due to large-scale structure along the line of sight, can convert some of the curl-free polarization pattern at the surface of last scatter into a curl component, even in the absence of gravitational waves [Zaldarriaga & Seljak 1998]. This cosmic-shear-induced curl can thus be confused with that due to gravitational waves. In principle, the two can be distinguished because of their different power spectra, as shown in Fig. 2, but if the IGW amplitude is small, then the separation becomes more difficult. Lewis et al. (2002), Kesden et al. (2002), and Knox & Song (2002) showed that when the cosmic-shear confusion is taken into account, the smallest detectable inflationary energy scale is 4 × 10¹⁵ GeV.

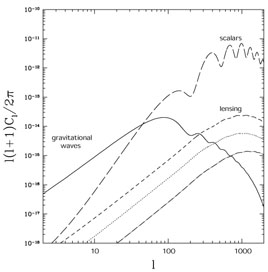Figure 2. CMB polarization power spectra. The long-dashed curve shows the dominant polarization signal in the gradient component due to scalar (density) perturbations. The solid line shows the maximum allowed curl polarization signal from the gravitational-wave background, which will be smaller if the inflationary energy scale is smaller than the maximum value allowed by COBE of 3.5 × 1016 GeV. The dashed curve shows the power spectrum of the curl component of the polarization due to CS. The dotted curve is the CS contribution to the curl component that comes from structures out to a redshift of 1; this is the level at which low-redshift lensing surveys can be used to separate the CS-induced polarization from the IGW signal. The dot-dashed line is the residual when lensing is separated with a no-noise experiment and 80% sky coverage. From Kesden et al. (2002).

The deflection angle due to cosmic shear can in principle be mapped as a function of position on the sky by studying higher-order correlations in the measured CMB temperature and polarization [Seljak & Zaldarriaga 1999, Hu 2001a, Hu 2001b, Hu & Okamoto 2002, Cooray & Kesden 2002]. If this deflection angle is determined, then the polarization can be corrected and the polarization pattern at the surface of last scatter can be reconstructed. Kesden et al. (2002) and Knox & Song (2002) found that with such a reconstruction, the cosmic-shear-induced CMB curl component can be reduced by roughly a factor of ten, as indicated in Fig. 2. This then leads to a smallest inflationary energy scale that will produce a detectable IGW signal in the CMB polarization curl. The conclusion is that the CMB-polarization signature of IGWs will be undetectable, even with perfect detectors, if the energy scale of inflation is smaller than 2 × 10¹⁵ GeV.

Let us now suppose that this curl component was indeed detected. It would immediately tell us that the vacuum-energy density during inflation was (10^15-16 GeV)⁴, and thus that inflation probably had something to do with grand unification. However, there is possibly more that we can learn. Since the unifying high-energy physics responsible for inflation presumably encompasses electroweak interactions as a low-energy limit, and since the weak interactions are parity violating, it is not unreasonable to wonder whether the physics responsible for inflation is parity violating. Lue et al. (1998) and Lepora (1998) showed how parity-violating observables could be constructed from a CMB temperature-polarization map. Moreover, examples were provided of parity-violating terms in the inflaton Lagrangian that would give rise to such signatures by, for example, producing a preponderance of right- over left-handed gravitational waves.