The simplest single-scalar-field inflation models predict that primordial perturbations have nearly Gaussian initial conditions. A small degree of non-Gaussianity generally arises from self-coupling of the inflaton field, but this is expected to be very tiny [Salopek et al. 1989, Salopek 1992, Falk et al. 1993, Gangui et al. 1994, Gangui 1994]. More complicated models of inflation, such as two-field [Bartolo et al. 2002], warm [Gupta et al. 2002], or curvaton [Lyth et al. 2002] models may have small deviations from perfectly Gaussian initial conditions, and higher-order calculations of perturbation production suggest that non-Gaussianity may be significant even in slow-roll models [Acquaviva et al. 2002]. Although it is difficult, if not impossible, to predict the exact amplitude and precise form of non-Gaussianity from inflation, it is certainly reasonable to search for it.
Perhaps the most intuitive place to look for primordial
non-Gaussianity is in the CMB. Since the CMB temperature
fluctuations probe directly primordial density perturbations,
non-Gaussianity in the density field should lead to
proportionate non-Gaussianity in the temperature maps. So, for
example, if the primordial distribution of perturbations is
skewed, then there should be a skewness in the temperature
distribution. Alternatively, one can study the effects of
primordial non-Gaussianity in the distribution of mass in the
Universe today. This should have the advantage that density
perturbations have undergone gravitational amplification and
should thus have a larger amplitude than in the early Universe.
However, we must keep in mind that the matter distribution today
is expected to be non-Gaussian, even if primordial perturbations
are Gaussian. This can be seen just by noting that
gravitational infall can lead to regions - e.g., galaxies or
clusters - with densities of order 200 times the mean density,
while the smallest underdensity, a void, has a fractional
underdensity of only -1. However, non-Gaussianity in the galaxy
distribution from gravitational infall from Gaussian initial
conditions can be calculated fairly reliably (for an excellent
recent review, see, e.g.,
Bernardeau et
al. (2002)),
and so the distribution today can be checked for consistency with
primordial Gaussianity. In verdeone, we
studied the relative sensitivity of galaxy surveys and CMB
experiments to primordial non-Gaussianity. We considered
two classes of non-Gaussianity: in the first,
the gravitational potential is written
(x, t) =
g(x, t) +
g2(x, t), where
g(x) is a Gaussian random field (so
becomes Gaussian as
0); such a
form of non-Gaussianity arises
in some inflation models. In the second, the
fractional density perturbation is written
(x, t) =
g(x, t) +
g2(x, t); this
approximates the form of non-Gaussianity expected from
topological defects. We then determined what the smallest detectable
would be for
both cases for future galaxy surveys and for CMB experiments. We
found that in both cases the CMB would provide a more sensitive
probe of .
Conversely, if the CMB turns out to be
consistent with primordial Gaussianity, then for all practical
purposes, the galaxy distribution can safely be assumed to arise
from Gaussian initial conditions.
Experimentally, the bispectrum from 2dF [Verde et al. 2002] and the Sloan Digital Sky Survey [Szapudi et al. 2002] have now been studied and found to be consistent with Gaussian initial conditions. A tentative claim of non-Gaussianity in the the COBE-DMR maps [Ferreira et al. 1998] in great excess of slow-roll-inflationary expectations [Wang & Kamionkowski 2000, Gangui & Martin 2000] was later found to be due to a very unusual and subtle systematic effect in the data [Banday et al. 2000].
The abundances of clusters provide other avenues toward detecting primordial non-Gaussianity. Galaxy clusters, the most massive gravitationally bound objects in the Universe presumably form at the highest-density peaks in the primordial density field, as indicated schematically in Fig. 3. Now suppose that instead of a Gaussian primordial distribution, we had a distribution with positive skewness, as shown in Fig. 3. In this case, we would expect there to be more high-density peaks, even for a distribution with the same variance, and thus more clusters [Robinson et al. 2000]. Thus, the cluster abundance can be used to probe this type of primordial non-Gaussianity.
 |
Figure 3. The solid curve shows a Gaussian distribution P(y) with unit variance, while the broken curve shows a non-Gaussian distribution with the same variance but 10 times as many peaks with y > 3. This illustrates (a) how the cluster abundance can be dramatically enhanced with long non-Gaussian tails (since clusters form from rare peaks); and (b) that the dispersion of y for y > 3 is much larger for the non-Gaussian distribution than it is for the Gaussian distribution, and this will lead to a larger scatter in the formation redshifts and sizes of clusters of a given mass. From ourclusters. |
Just as clusters are rare objects in the Universe today,
galaxies were rare at redshifts z
3. In
[Verde et
al. 2001a],
we considered the use of abundances of
high-redshift galaxies as probes of primordial
non-Gaussianity. We also found an expression that relates the
excess abundance of rare objects to the
parameter in
the models discussed above and were thus able to compare the
sensitivities of cluster and high-redshift-galaxy counts and the
CMB to non-Gaussianity in the models considered above. We found
that although the CMB was expected to be superior in detecting
non-Gaussianity in the gravitational potential, the
high-redshift-galaxy abundances may do better with
non-Gaussianity in the density field.
 |
Figure 4. Mass and formation-redshift
contours in the size-temperature plane for
|
In addition to producing more clusters, such a skew-positive distribution might change the distribution of the properties of such objects. In ourclusters, we considered the size-temperature relation. If we model the formation of a cluster as a spherical top-hat collapse, then the virial radius and the virial temperature can be determined as a function of the halo mass and the collapse redshift. We then modeled the x-ray-emitting gas to relate its size and temperature to the virial radius and temperature of the halo in which it lives in order to obtain better estimates for the x-ray isophotal radii and x-ray temperatures that are measured. Fig. 4 shows resulting contours of constant mass and constant collapse redshift in the cluster size-temperature plane. As shown there, halos that collapse earlier should lead to hotter and smaller clusters, and more massive halos should be hotter and bigger. If the primordial distribution is skew-positive, then the halos that house clusters will collapse over a wider range of redshifts, and as indicated in Fig. 5, this will lead to a broader scatter than in the size-temperature relation than is observed. In this way, primordial distributions with a large positive skewness can be constrained.
 |
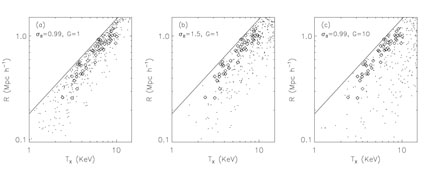Figure 5. (a) Size-temperature distribution
for LCDM and
|
0 = 0.3
and h = 0.65 obtained
from the spherical-top-hat model of gravitational collapse
discussed in the text. It is clear from the figure that a
narrow (broad) spread in the formation redshift will yield a tight
(broad) size-temperature relation. For larger
8 = 0.99 and
Gaussian initial conditions. Each dot
represents a simulated cluster, while the diamonds are
data from M00. The line shows the size-temperature
relation expected for clusters today. Panel (b) shows the same
except that here we use