The final probe of inflation that we will discuss here is motivated by the galactic-substructure problem. N-body simulations of structure formation with a standard inflation-inspired scale-free spectrum of primordial perturbations predict far more substructure, in the form of dwarf galaxies, in galactic halos than is observed in the Milky Way halo, as indicated in Fig. 8 [Klypin et al. 1999, Moore et al. 1999]. Although a number of possible astrophysical mechanisms for suppressing this small-scale power have been proposed (e.g., Bullock et al. (2000), Benson et al. (2002), Stoehr et al. (2002)), there is still no general consensus on whether they are sufficiently effective to eliminate the problem.
 |
 |
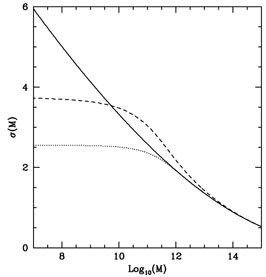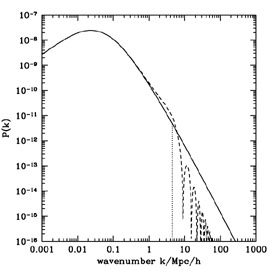
Figure 6. The upper panel shows the power spectrum for an LCDM model (solid curve), for a model in which the power spectrum is arbitrarily cut off at k = 4.5 h Mpc-1 (dotted curve), and the broken-scale-invariance inflation model (dashed curve). The lower panel shows the rms mass fluctuation as a function of the enclosed mean mass M for these three models. From Kamionkowski & Liddle (2000). |
Another possible explanation of the observed dearth of dwarf
galaxies is a small-scale suppression of power that could occur
if the inflaton potential has a sharp feature, like that shown
in Fig. 7
[Kamionkowski &
Liddle 2000,
Yokoyama 2000].
According to inflation, primordial density perturbations are
produced by quantum fluctuations in the inflaton, the scalar
field responsible for inflation. Moreover, the details of the
power spectrum P(k) of density perturbations (as shown in
Fig. 6) is determined by the shape
V(
) of the inflaton
potential. The amplitude of a given
Fourier mode of the density field is proportional to the value
of V3/2 / V', where V' is the first
derivative of the
inflaton potential, at the time that the perturbation exited the
horizon. In most models, the inflaton potential is smooth and
this leads to a power spectrum of perturbations that is very
nearly a power law - Ref.
[Lidsey et
al. 1997]
explains very
nicely how the amplitude and slope of the inflaton potential can
be reconstructed in this case.
 |
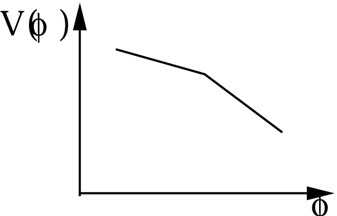Figure 7. An inflaton potential with a break in the first derivative. |
However, suppose that for some reason there is a break in the
inflaton potential, as shown in Fig. 7, and the
slope increases suddenly as the inflaton roles down the
potential. In this case, V' increases suddenly, and
since the density-perturbation amplitude is
1/V', the
density-perturbation amplitude on small scales (those that exit
the horizon last) will be suppressed, as indicated by the dashed
curve in Fig. 6. The wiggles in the dashed curve
are ringing in Fourier space that results from the sharpness of
the feature. If it is smoothed out, then a power spectrum more
like the dotted curve in Fig. 6 becomes possible.
 |
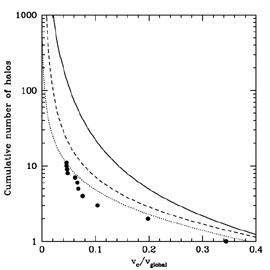Figure 8. The cumulative number of mini-halos for the power spectra shown in Fig. 2 as a function of the circular speed vc of the halo divided by the circular speed vglobal of the Galactic halo. The points show the Milky Way satellites. From Kamionkowski & Liddle (2000), after Moore et al. (1999). |
With the three power spectra in the upper panel of
Fig. 6, the rms mass fluctuation
(M) on a
mass scale M can be calculated, as shown in the lower panel of
Fig. 6. With the scale-invariant spectrum,
(M) keeps rising
as we go to smaller and smaller masses,
leading to substructure on smaller scales. However, if power is
suppressed on small scales, then
(M) ceases to
rise (or rises only very slowly) at small M implying the absence (or
suppression) of halos of these small masses.
Given (M) for
these three power spectra, the abundance
of sub-halos in a typical galaxy-mass halo of 1012
M
can be
calculated with the extended Press-Schechter
formalism. Results of this calculation are shown in
Fig. 8. As a check, the approximation
reproduces well
the numerical-simulation results for the scale-free spectrum.
For the power spectra with broken scale invariance, the
abundance of low-mass substructure is reduced and brought into
reasonable agreement with the observed ten or so Milky Way
satellites, without violating consistency with constraints from
the Lyman-alpha forest
[Kamionkowski &
Liddle 2000,
White & Croft
2000].
Is such a break to be expected theoretically? Probably not, and there are probably simpler explanations for the shortfall that involve more conventional astrophysics. Still, these calculations show that by studying and understanding galactic substructure, we learn about the shape of the inflaton potential toward the end of inflation in a way that complements the information from earlier epochs of inflation that comes from larger scales.