3.6. Absolute Magnitudes and Linear Diameters of Double Galaxies

The calculation of the luminosity function for double galaxies per unit volume and their distribution function by linear diameter meets with a number of difficulties produced by a variety of selection effects. Deriving the luminosity function (M₁, M₂) from the catalogue ^*(M₁, M₂), where M₁ and M₂ are the absolute magnitudes of the brighter and fainter components of the pair, has already been examined analytically by White and Valdes (1980) and Arakelyan (1983a, b), but even with the strong simplification of an analytical approach, notable difficulties have appeared.

In this section, we will limit our discussion to the observational data and estimate the role of the most basic selection factors in determining the distribution of double galaxies by absolute magnitude.

The distribution of 1170 double galaxies in the catalogue according to measured radial velocity is shown as a histogram in figure 14. From the given photometric limit of the catalogue, it has a shape comparable to that of the luminosity function (M₁, M₂) and, to a lesser extent, displays the selection criteria for pairs. The most luminous objects in the catalogue have a velocity V₀ 15000 km/s. The mean radial velocity of double galaxies is 6350 km/s. The dashed line in the figure indicates the distribution of model galaxies with the postulated luminosity function (3.2). It describes the distribution of double systems including only the brighter catalogue component. The mean velocity for these `half-pairs' is the nearly matching 6190 km/s. The full line indicates the distribution of model pairs which appear in the sample with both components brighter than magnitude 15.7. The mean radial velocity of these is 2890 km/s, or, to put it another way, their effective depth in space is reduced by more than a factor of two in comparison with the `half-pairs'. The strong selection against distant pairs occurs among the model sample because of the assumption of independence of the absolute magnitudes of the two pair members. To bring the model and catalogue distributions in figure 14 into agreement for independent M₁ and M₂ it would be necessary to increase the luminosity of the components of the M-pairs by a factor of four or five, but since the actual absolute magnitudes of double galaxies exhibit a strong correlation, the expected distribution changes to the one shown in the dashed line in figure 14.

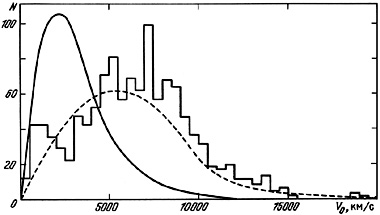Figure 14.

Note further the observed excess in the number of catalogue pairs with radial velocities below 2000 km/s. Apparently this is explained by the fact that many nearby double systems belong to the local supercluster of galaxies. Additional peaks are noticeable in the histogram N(V₀), which agree with the presence of the Perseus and Coma clusters.

The role of various selection effects may be estimated from the data in Table 7, which presents the distribution of the number of real and model double galaxies in absolute magnitude bins of width 0.5 magnitude. The second and third columns of the table show the number of catalogue galaxies broken down into brighter and fainter pair components. The absolute magnitudes are presented on Holmberg's photometric system, m_Ho^c. The distributions of the members of model pairs are given in the fourth through the eighth columns, which are the same as given in Table 6. The last line of the table gives the mean value of the absolute magnitude and its standard deviation for every sub-sample.

The combination of the selection factors we have described has the net effect that in the mean, galaxies from the M-pairs are fainter (-18.72^m) than single galaxies (-19.28^m). Examining the data in the second or third columns of Table 7 we see that the catalogue pairs have a markedly higher luminosity than the model ones. Part of this difference may result from an incorrect choice of the zero point in the absolute magnitude scale of the M-galaxies, or from a real luminosity excess in the catalogue pairs. To examine this we will use as a control the catalogue of isolated galaxies of Karachentseva (1973).

We first point out several salient features of the selection of the galaxies for this catalogue. Galaxies with angular diameter a₀ are considered isolated if any significant neighbours with diameters a_i, a₀/4 < a_i < 2a₀ have an angular separation from the galaxy under consideration greater than 20a_i. Such a basic definition of a zone of avoidance around a galaxy has a characteristic radius ~ 400 kpc. The catalogue of isolated galaxies (total number of objects, n = 1051) covers the same area of the sky and has the same limiting magnitude m = 15.7 as does the catalogue of pairs. At the present time, the program of measuring radial velocities for the isolated galaxies has not been completed. Only for 300 objects with known radial velocities do we have information on the absolute magnitudes M_Ho^c and linear diameters A₂₅, reduced to the standard system following the scheme given in section 2.2.

The mean absolute magnitude of the 300 isolated galaxies is <M_Ho^c> = - 19.68^m ± 0.09^m, with standard deviation _M = 1.52^m. For the fainter and brighter components of K-pairs we have for comparison <M_Ho^c> = - 19.91^m ± 0.05^m, _M = 1.32^m, and <M_Ho^c> = - 20.57^m ± 0.05^m, _M = 1.13^m. As we see, not only the brighter but also the fainter members of pairs are characteristically brighter in luminosity by comparison with isolated galaxies. To satisfy the mean value <M> simultaneously in the model and catalogued isolated galaxies, it would be necessary to shift the zero point of the luminosity function by -0.40 magnitudes ⁽³⁾.

The distribution of 1170 double galaxies from the catalogue by absolute magnitude is shown as the histogram in figure 15. The straight lines illustrate the sample luminosity function as given by (3.2), increased by the volume factor 10^-0.6M. The distribution of 300 isolated galaxies is shown as the points. These data may be interpreted either as indicating different luminosity functions for double and single galaxies, or as a shift between them. To examine this question, it is necessary to understand all of the selection effects which operate on the distribution of absolute magnitudes of catalogue pairs. Computer modelling can indicate the magnitude and direction of selection effects, but our model, which has ignored the observed correlation between absolute magnitudes of double galaxies, is too simple to establish any systematic differences in (M) between double and single galaxies.

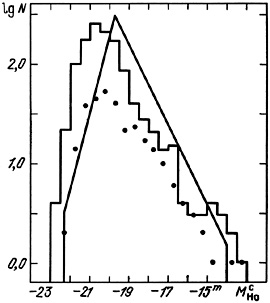Figure 15.

For quantitative estimates, we note that the components of double systems (<M> = - 20.24^m ± 0.04^m) have by comparison with isolated galaxies (<M> = - 19.68^m ± 0.09^m) a mean luminosity excess of 10^{0.4 × 0.56} 1.7. An even stronger difference (M = - 0.88^m) was found by White and Valdes (1980) for a sample of 63 Turner pairs. This increase in luminosity for double galaxies may arise from the same basis as other specific properties of paired systems.

Aside from their absolute magnitudes, an equally important integral characteristic of galaxies is their linear diameters. Figure 16 shows the distribution of double galaxies by linear diameter, measured at the standard isophote 25^m/sq.arc sec. Just as with the luminosity function, this distribution is affected by various apparent selections which deserve special examination and serve to limit our treatment of the problem. The mean diameter of the components of the pairs is 24.3 ± 0.7 kpc, with a standard deviation _A = 11.9 kpc. For 300 isolated galaxies, <A₂₅> = 24.7 ± 0.9 kpc, and _A = 14.9 kpc. From this, with an accuracy limited by selection effects, we see that the linear diameters of double galaxies are not significantly different from those of single systems.

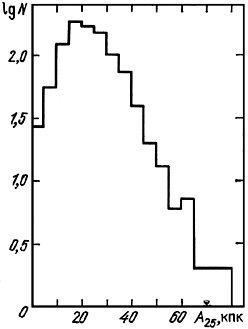Figure 16.

³ in the system m_Ho, not including the effects of light absorption because they are satisfactorily close to zero. Back.