One of the first methods for estimating the masses of double galaxies was worked out by Page (1952, 1960, 1961, 1962). Page viewed the motion of two galaxies as that of material points on circular trajectories at a fixed distance. Such a Keplerian approach was carried further in articles by Holmberg (1954), Karachentsev and Shcherbanovsky (1970), Karachentsev (1970b, 1974, 1976, 1981d) and Noerdlinger (1975). The case of the motion of two galaxies with a more general mass distribution was analysed by Turner (1976b), Peterson (1979b) and White (1981). A comparison of the various approaches to estimating the mass of a double system was presented in the review by Faber and Gallagher (1979).
We will first assume that the components of pairs with given masses move on circular orbits with given velocity V12 and spatial separation r. The sum of the component masses may be determined from Kepler's second law
 |
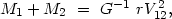(4.1) |
where G is the gravitational constant. We transform from V12 and r to the observed quantities, which are the projected velocity difference along the line of sight
 |
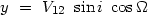(4.2) |
and the projected separation on the plane of the sky
 |
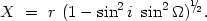(4.3) |
Here i is the angle between the plane of the orbit and the plane
of the sky and 
is the
angle between the line connecting the components and
the line of sight. These geometrical considerations are clarified in
figure 17.
 |
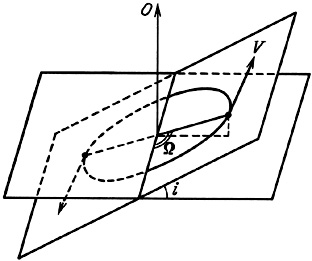Figure 17. |
We will make the obvious assumption that double galaxies exhibit a
random distribution of orientations with respect to the line of sight.
Then, the simultaneous distribution of the random quantities i
and will have the form
 |
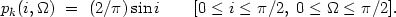(4.4) |
Introducing the notion of a geometrical projection factor
 |
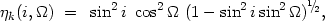(4.5) |
we may re-express the total mass of a pair as
 |
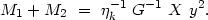(4.6) |
For circular motion the mean value of the projection factor is
 |
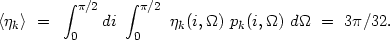(4.7) |
The desired combination of observed quantities
 |
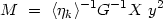(4.8) |
is an estimate of the total mass of a pair. For the convolution when double galaxies have various distribution functions for the total mass, and random orientations of their separation vector with respect to the line of sight, the mean value of the mass is equivalent to the mean value of an ensemble of pairs:
 |
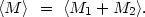(4.9) |
In each individual case, the estimate of the orbital mass of a pair may differ markedly from its true mass. Incorporating (4.5) and (4.4), we derive for the geometric correction factor a distribution function
 |
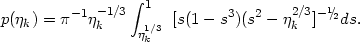(4.10) |
Results from the numerical integration of (4.10) are presented in
figure 18.
As is shown there, the distribution of projection factors has a very
asymmetric form, with a maximum at
k =
0 and an extended tail to
k = 1.
The actual transformation between the total mass of a pair and its estimate
contains uncertainties, in addition to the orientation factors, because
of errors in measurement of the radial velocity for the galaxies.
 |
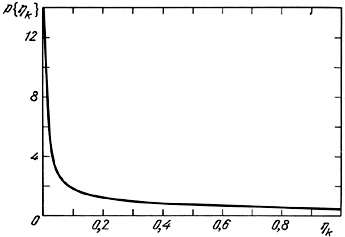Figure 18. |
It is easy to show that for the general case of elliptical motion with orbital eccentricity e, the projection factor is
 |
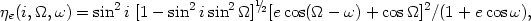(4.11) |
where 
indicates the
angle between the major axis of the orbit and
the line of sight, and the angles i and
were explained above.
For a random orientation of orbits the distribution for these three
angles is
 |
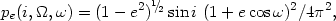(4.12) |
where [0 
i
/2, 0
2, 0
2].
By using (4.11) and (4.12) it is possible to express the mean values of
the projection factors including orbital eccentricity:
 |
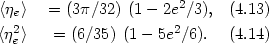(4.13) (4.14) |
These expressions were presented by
Yakimov (1968) and
Karachentsev and
Shcherbanovsky (1970).
It follows from (4.13) that the mean orbital mass estimator is minimized for
circular trajectories.
If the motion of galaxies in pairs is strongly radial, then, by comparison
with (4.8), the mean mass estimator will be larger by a factor of three.
In what follows we shall use the orbital mass estimator (4.8) with a
mean projection factor of
(3 / 32); that is, we
will consider double galaxies to have circular orbits.
Justification for this assumption will be given below.
Figure 19 shows the distribution of 585 double systems from the catalogue according to orbital mass estimators. Attention is called especially to the enormous range in the values of M, approaching ten orders of magnitude. For comparison, note that the maximum range of luminosity of the various galaxies in pairs does not exceed four orders of magnitude. Besides the true range of masses, the spread in projection factors and the inclusion of false pairs in the catalogue sample contribute to the dispersion in mass estimators.
 |
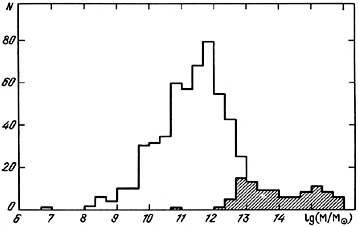Figure 19. |
To substantiate the role of fictitious double systems we return to the data for model pairs. While performing the computer generation of the apparent distribution of galaxies and the subsequent selection of double systems satisfying the isolation criterion, we did not incorporate gravitational interactions between galaxies. Ignoring this, the mutual velocities and separation of galaxies in M-pairs may be used for formal mass estimates following (4.8). The distribution of 301 modelled pairs by orbital mass estimators is presented in figure 20. Physical pairs are presented with double hatching, members of groups and clusters with single hatching, and optical pairs are the open histogram.
 |
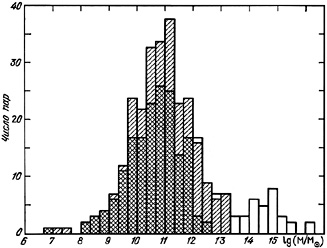Figure 20. |
Comparing the distributions of catalogue and model pairs shows general
agreement. As proposed above, the very largest orbital mass estimates
(M > 2 × 1013
M
)
occur among fictitious pairs; that is, they
occur among the sub-sample of optical doubles.
Physical pairs and optical pairs are well separated on the log M
scale, which makes it easy to exclude false pairs by using a critical
value for the orbital mass estimator. However, this simple picture
breaks down because the basic isolation criterion
of the catalogue is also satisfied by a large number of group and cluster
members for which these formal mass estimators occur in the range
(107 - 2 × 1013)
M.
A separate number of pseudo-pairs occurs in the range of values
(1012 - 2 × 1013)
M,
with about the same separation between peaks which distinguishes physical
and optical double systems.
In calculating the masses of double galaxies, the masquerading role of
system members is usually ignored which leads to overestimates of the
mean orbital mass, by nearly an order of magnitude.
Many authors view this mistaken result as evidence for the presence of
massive invisible haloes around galaxies.