4.2. Mass-to-Luminosity Ratios and Projection Factors

It is known that galaxies vary in both luminosity and mass over ranges of hundreds to thousands. This cannot be said about the ratio of the integrated mass of a galaxy to its integrated luminosity, which depends only weakly on the absolute magnitude of the objects and is confined to a relatively small range of values. The data fully support the proposition that, for double galaxies as well, the ratio of the total mass of the components to their total luminosity, f₀ = (M₁ + M₂) / (L₁ + L₂), is limited to a rather small range of values.

By way of contrast to f₀, the estimator of the ratio of orbital mass to luminosity

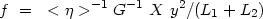(4.15)

exhibits marked variation from pair to pair due to the role of the projection factor, . The distribution of 585 double systems according to estimates of f is shown on a logarithmic scale in figure 21. We will use these data to estimate the distribution of pairs according to the true mass-to-luminosity ratio, f₀.

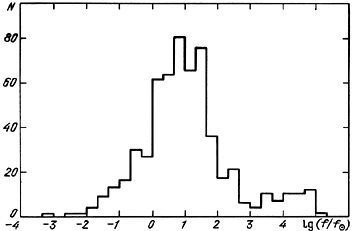Figure 21.

For sufficiently large samples of double galaxies with random orientations to the direction of observation, an estimate of f may be viewed as the convolution of two independent quantities,

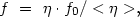(4.16)

substituting the integration over the entire number of pairs for the integration over viewing angles. For mutually uncorrelated quantities and f₀, the following relation may be obtained between the n-th moments of the distribution

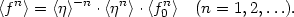(4.17)

If the motion of double galaxies is circular, these moments of the projection factors become Gamma functions of the given argument:

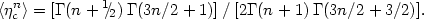(4.18)

In the case of purely radial motion of the galaxies, it is easy to show that

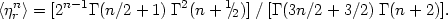(4.19)

Analogous expressions for the moments of the projection factor may be obtained from (4.11) and (4.12) for the general case of elliptical motion with fixed orbital eccentricity e.

Therefore, equation (4.17) allows one to obtain the moments of the true distribution of the physical quantity f₀ from the moments of f, computed from observations, if the type of the orbital motion of double galaxies is known. Knowing the moments f₀ⁿ it is possible to establish the standard deviation of the true distribution p(f₀).

However, the relation (4.17) between moments of observed and true mass-to-luminosity ratios describes only an idealized situation in which errors of measurement of the radial velocities of the galaxies are negligibly small. In reality the differential radial velocity of the components of a pair may be viewed as the sum of the true difference, y₀, and random errors of measurement u:

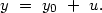(4.20)

Assuming that, for the total sample of pairs, y₀ and u are mutually independent random variables, we have from (4.15) and (4.20)

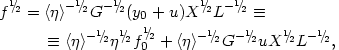(4.21)

where L = L₁ + L₂ is the total luminosity of the pair components. Together with the simple relation (4.17), we now have a relation between adjacent moments:

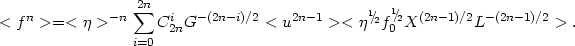(4.22)

It is obvious that the projected separation between double galaxies and the orientation factor of the pair are not, in fact, independent quantities. In addition, the pair luminosity L and the mass-to-luminosity ratio f₀ may be correlated with one another and with the relative separation of the components, due to the physical properties of double galaxies, such as extensive envelopes around them or, in fact, the previously discussed selection effects. Therefore, the practical application of expression (4.22) is a complex matter.

The distribution of errors in radial velocity may be accurately described as a symmetric function (i.e. <u> = 0) and for its first moment, from (4.22), we have

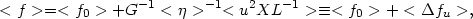(4.23)

where f_u indicates the correction to the mass-to-luminosity ratio required by errors in the measured radial velocity. To go further, we introduce the limiting assumption that the quantities X, L, , and f₀ are mutually uncorrelated. Then, the recurrence relation (4.22) becomes

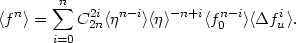(4.24)

Thus, having calculated the sample moments of the estimator f for the double galaxies and incorporating the correction f_u for errors in radial velocities, we may finally establish from (4.24) the mean value, dispersion, skewness, and kurtosis of the true quantities f₀ for a given type of orbital motion, and from this establish the form of the distribution p(f₀).

Before moving on to this question, we will deal with the problem of possible selection in the distribution of pairs according to viewing angle. Turner (1976b) and Faber and Gallagher (1979) showed that the assumption of a mean projection factor established according to (4.7) requires a significant correction for the effects of a non-random orientation of pairs. This comes from the fact that the basic selection of double galaxies from their relative angular separations operates against the selection of wide pairs. According to the estimates of this effect by these authors, neglect of this correction reduces the mean derived orbital mass by factors of a few.

This assumption about anisotropic selection may be examined using the model pairs. For each M-pair, both the true separation r and its projection X are known. For a uniform random orientation of pairs and uniform selection according to angular separation, the basic relation is <X / r> = / 4 0.785. For the sample of M-pairs satisfying the isolation criterion, the mean value of this ratio is in fact 0.763, which satisfies the prediction, within the statistical errors. It follows that the selection of double galaxies on the basis of their isolation does not introduce a noticeable anisotropy in the apparent orientation of the pair, and systematic errors in estimates of the mean orbital mass should then be negligible.

In order to establish the density distribution of pairs according to their mass-to-luminosity ratio, p(f₀), it is necessary to exclude false double systems from the sample. The desired rule for this, apparently, does not exist. As shown by the methods above using random distributions, the number of optical and non-isolated double systems in the catalogue is about 43%. Optical pairs having formal estimates of f = 10³ - 10⁶ are easy to distinguish from physical pairs, but the problem of dealing with members of groups and clusters is much more difficult even when they satisfy the isolation criteria for the catalogue. For characteristic separations ~ 50 kpc and peculiar velocities ~ 400 km/s, pseudo-pairs that are close in projection have values occupying the rather large range f = 100 - 1000. Therefore, for false, non-isolated pairs we apply the criterion f > f^* = 100. On this basis, we may exclude from the catalogue 98/585 17% of the objects, which is 2.5 times fewer than the fraction predicted from the modelling. We deal further with only this sub-sample, consisting of 487 pairs with f < 100, realising, however, that it may contain a significant contribution from non-isolated systems. (If we further restrict the adopted boundary between physical and false pairs, say f^* = 50, then we risk excluding from the analysis actual massive pairs which would satisfy the same selection.)

The distribution of these 487 pairs with f < 100 is presented in figure 22. The histogram shows the distribution of f without regard to errors in the radial velocities. The points indicate the distribution of the corrected estimate f_c = f - f_u. Note that the displayed quantity f_c includes pairs for which the errors in measurement of the radial velocity difference approach the absolute value of the measured difference (_y > y). Comparison of these distributions shows a significant effect of the error _y on estimates of the mass. As already remarked in discussing the episodic measurement of radial velocities for pairs performed by various authors, considering the known errors it is just barely possible to establish the function p(f₀).

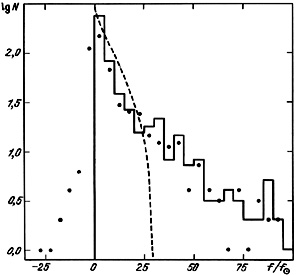Figure 22.

Proceeding to pare down and improve the observational material, we further exclude from the analysis pairs for which the orbital mass-to-luminosity ratio exhibits a large expected error. Among 487 pairs we identified 286 having a correction f_u < 2 (sub-sample A). As a control we also examined sub-samples B and C which are limited respectively by the criteria f_u < 5 and f_u < 10. The small corrections resulting from errors in measured velocities weaken the role of any possible correlations between random changes in expression (4.22), permitting the use in its place of the simplified expression (4.24), which does not incorporate mixed moments. The basic characteristics of these three sub-samples are presented in Table 8, which lists n, the number of pairs; f_u, the mean value of the correction resulting from velocity errors; < f >, the mean corrected estimate of the orbital mass-to-luminosity ratio; <f²_*> / <f²>, the characteristic dispersion; ₁(f )= <f³_*>² / <f_*²>³, the normalised index of skewness; and ₂(f )= <f⁴_*> / <f_*²>², the normalised index of kurtosis, where <f^k_*> indicates the central limit of the k-th moment.

To estimate the moments <f₀^k> we proceeded as follows. Using (4.11) and (4.12) for a series of values of the orbital eccentricity e (0.05, 0.15, 0.25 ... 0.95), we generated a distribution of projection factors using Monte Carlo methods. For each value of e, we generated 10⁵ trial values for the moments <^k>. Note that for purely circular and purely radial motion the moments of the projection factor have the analytical forms (4.18) and (4.19). Together with (4.24) the sample moments <f^k> and f^k_u were finally transformed into moments of the true mass-to-luminosity ratio <f₀^k>. Analytical expressions for the distribution p(f₀) were produced with the aid of Pearson diagrams (Gunn and Shapiro, 1967) incorporating the sample values of the skewness and kurtosis indices ₁ and ₂. The results of these calculations are presented in Table 9 and in Figure 23.

The Pearson diagram, figure 23, requires some explanation. Two of its coordinates are the dimensionless indices of skewness ₁ and kurtosis ₂ which uniquely characterize the form of the distribution. For example, uniform and normal distributions appear on the (₁, ₂) diagram as the points (0, 1.8) and (0, 3). An exponential distribution on this diagram appears at point (4, 9). A gamma distribution has the form of a straight line, shown as the dot-dash line, extending beyond the two last points. A log-normal distribution is the light solid line below this. The shaded part of the Pearson diagram indicates a critical zone [₁ < 0 and ₂ < ₁ + 1], where no actual distribution of the desired form can exist. Between this critical line ₂ = ₁ + 1 and the line corresponding to gamma functions is the region of beta distributions. This consists of zones for the U-like or bi-modal, and J-like or uni-modal, distributions. The last of these is shown as the short dashed curve in figure 23.

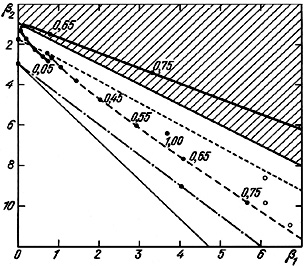Figure 23.

In the lower right corner of figure 23, the three open circles indicate the properties of the distributions p(f ) for sub-samples A, B and C, using the data from Table 8. All of the values ₁ and ₂ for the projection factors (second and third lines of Table 9) occupy a uniform sequence in the Pearson diagram, shown as the narrow dashed line. The points along it indicate the values expected for various orbital eccentricities. As will be shown later, the skewness and kurtosis of the distribution of rapidly increase with the value of the eccentricity, e. The function p () for any desired e will form a J-type or beta distribution. This distribution for circular orbits was presented in figure 18. We remark on one final property. For e 0, the parameters ₁ and ₂ asymptotically approach the values for pure circular motion. However, for e 1, elliptical motion does not have as its asymptotic case the values for pure radial motion. The distribution of projection factors for radial motion forms a point at coordinates ₁ = 3.66 and ₂ = 6.40. Such a `degeneracy' for radial motion is characteristic only of the higher order moments, since, according to (4.13) and (4.14), the first two moments do not show such a distinction.

We return to the question of the form of the true distribution p (f₀). Its trajectory on the Pearson diagram is shown by the sequence of points for various values of e, connected by the dashed line. To avoid cluttering figure 23 we present this information only for the basic sub-sample, A. The trajectories of sub-samples B and C may easily be produced from the data in Table 9. The values of ₁ and ₂ for e = (0.0 - 0.30) lie in the region of the J-like beta distributions. On going to more elliptical orbits, e = (0.30 - 0.55), the distribution lies in the region which is U-shaped, and for e > 0.55 it appears in the critical region. In other words, a hypothesis of orbital motion with e > 0.55 does not have any imaginable physical significance.

From the data in Table 9 it is apparent that inclusion in the samples of objects with poorly measured radial velocities only serves to narrow the permitted range of orbital eccentricities. For pairs with f_u < 5, the function p(f₀) has a U-form (except for e < 0.35), and for the sub-sample with f_u < 10, all possible values of the eccentricity lie in the forbidden region. Therefore, the observed data point towards orbital motions of double galaxies characterized by small values of the eccentricity (e < 0.55). To assign a definite value and to limit discussion of the M/L distribution of pairs, we will assign them the value for almost circular orbits, with e < 0.30.

For calculation we will adopt the assumption presented above of a pure circular motion of galaxies in pairs. Then, after calculation of the parameters ₁ and ₂, the derived distribution p (f₀) may be presented as

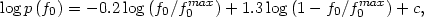(4.25)

where c is a normalisation constant and f₀^max = 30.0. Thus, the summed mass-to-luminosity ratios for double galaxies exhibit a distribution in the interval [0-30] with mean value <f₀> = 7.75 and standard deviation (f₀) = 6.47. A graphical representation of (4.25) is given as the short dashed line in figure 22.

We will note here one important circumstance. For a distribution of the form (4.25), technically the estimate of f for double systems may be shown to have a maximal value f^max = (32 / 3) f₀^max = 102, and this value practically matches the limit f^* = 100 which was selected as the basic boundary condition between physical and false pairs.

However, the analytical description of the function p (f₀) is not absolute. For the sample moments, a description of these distributions may only be approached in iterative steps. The real value of expressions for p (f₀) is limited not only by statistical fluctuations but also by inclusion in the sample of false pairs. Further, the form of the derived distribution will be affected by errors in measured radial velocities.

Ever-increasing interest has been evident in the calculation of the distribution of individual mass-to-light ratios p (f_in) for the components of pairs, with the help of (4.25) for the ratio of integrated mass to luminosity for double galaxies. We will illustrate this with some examples. Let pair members have identical luminosities and let their mass-to-luminosity ratios be uncorrelated. Then, the skewness and kurtosis indices of the distributions of f₀ and f_in will be given by ₁(f_in) = 2₁(f₀) and ₂(f_in) = 2₂(f₀). Having adopted ₁(f₀) = 0.75 and ₂(f₀) = 2.88 (sub-sample A, circular orbits), we find for p (f_in) values ₁ and ₂ agreeing with the log-normal distribution. According to Shaw and Reinhart (1973) just such a form is shown by the distribution of selected galaxies in their individual mass-to-light ratios. The question of comparing orbital and individual masses of galaxies will be examined in detail in section 4.4.