4.5. Does Hidden Mass Exist in Pairs of Galaxies ?

The comparison of the masses calculated from the motions of double galaxies to the sum of the masses calculated from the velocities of their individual components was first remarked by Zwicky (1933), so that the paradox of the missing or hidden mass has already celebrated its jubilee. The number of systems for which estimates of a virial mass are available grew rapidly. Page (1965) and Karachentsev (1966) presented in total about 100 systems of galaxies with measured masses and showed that estimates of the virial mass increased on moving from double and triple systems to groups, clusters, and super-clusters. The presence of unseen material in systems of galaxies was frequently taken to be a universal law of the extragalactic universe.

The hypothesis of unseen matter received further support from the work of Ostriker and Peebles (1973). By performing numerical experiments they showed that thin disks in spiral galaxies could only be stable in the presence of surrounding massive haloes or coronae. Further observational support for very massive haloes was presented by Einasto et al. (1974). Examination of the flat rotation curves in many spiral galaxies (Shostak and Rogstad, 1973, Roberts, 1975, Rubin et al., 1980) provided further support for the supposition of a large mass of invisible material outside the optical boundaries of galaxies.

However, there were also some observational data suggesting that this virial paradox is far from characteristic of all systems of galaxies. In many systems of low surface brightness an erroneous estimate of the virial mass may be obtained because of the low accuracy in measuring the radial velocity and the uncertain background subtraction when measuring the galaxy (Materne and Tamman, 1974, Fisher and Tully, 1975, Karachentsev, 1978). For NGC 3992 Gottesman and Hunter (1982) showed that the galaxy, despite its flat rotation curve, cannot have a massive halo because the relative velocities of its dwarf satellites at a distance of 60 kpc are very small.

In clusters of galaxies where the virial paradox is most marked and the ratio of virial masses to luminosity may reach 100 to 300 f the invisible mass is probably associated with the brightest member, a cD galaxy. Dressler (1979) performed a very difficult measurement of the stellar velocity dispersion in the cD galaxy in the cluster Abell 2029 and obtained the dependence _V(R) to distances of approximately 100 kpc from the center of the galaxy. Dressler viewed this result as indicating the presence of a massive halo around the cD galaxy. However, in accounting for Dressler's data, Tonry (1983) used a model for the distribution of f along the radius of the galaxy, incorporating an anisotropic velocity distribution. The very strongest argument concerning the presence of large masses in the vicinity of galaxies concerns the brightest member of the Virgo cluster, M87. The distribution of X-ray brightness on the basic assumption of hydrostatic equilibrium of the gas allows one to calculate the profile of the gravitational potential in the gas. According to Fabricant and Gorenshtein (1983) the mass-to-luminosity ratio in M87 rises from normal values ~ 10f in the central regions to ~ 180 at a distance of 90 kpc from the center. Analogous information on X-ray brightness profiles presented by Forman et al. (1985) was interpreted as showing the presence of massive haloes around other elliptical and lenticular galaxies.

Completing this extensive array of arguments for and against invisible haloes, we note several recent publications. Bahcall et al. (1982) examined various interpretations for flat rotation curves and came to the conclusion that the explanation of a constant rotation velocity at large distances may be more difficult than simple models with dark massive haloes with a mass distribution M(R) ~ R. Pryor and LeCar (1983) attempted to obtain flat rotation curves from a model of infalling gas from the intergalactic medium. The original arguments for massive haloes were re-examined by Tyson et al. (1984). By measuring a large number of faint galaxies, the authors searched for systematic effects in the orientation of such systems in the vicinity of much brighter galaxies. Interpreting such effects as due to gravitational lensing, Tyson et al. (1984) calculated the mean mass of field galaxies as <M> = 1.3 × 10¹¹ M. The authors maintain that their method is sufficiently simple, universal and free of uncertainties as to supercede other mass estimators. For an average field galaxy they found <f> 18 for H = 75 km/s/Mpc. This estimate allows the possibility of dark matter around galaxies with a typical distance R ~ 100 kpc, i.e., it strongly limits the mass of an invisible halo.

Now, we return to the problem of unseen mass in double systems of galaxies. Turner (1976b), Yahil (1977), White et al. (1983), and Sadler and Sharp (1984) investigated moderate-sized (n ~ 30 to 60) samples of isolated pairs and studied the correlations between the observed parameters, y, X, and L. They found that interactions in double systems agree very poorly with Keplerian models for the motion of point masses. As a specific alternative one may consider that the components of pairs are immersed in an extended massive medium, which induces a correlation between relative velocity, distance and luminosity. Even earlier, Einasto et al. (1974) considered the data on pairs as among the very strongest arguments for the hypothesis of massive haloes.

In studying the literature concerning invisible haloes around galaxies one may distinguish two basic situations: a) dark mass situated at moderate distances from the centers of galaxies in the range 1.5 to 2.0 R₂₅, thus accounting for the flat rotation curve observed to the optical radius of the galaxy, R₂₅. The total mass of the galaxy in this case may be increased by 1.5 to 2 times from its visible mass (the minimal hypothesis); b) invisible surrounding matter distributed on scales 10R₂₅, accounting for the motions of dynamically wide pairs with separations 100 kpc. The dark mass in this case exceeds the visible mass by an order of magnitude and may affect the cosmological parameter ₀ (the `maxi-halo' hypothesis).

We will examine first the latter, more radical, proposition. To limit the maxi-halo we may examine the marked correlation between the orbital mass-to-luminosity ratio of pairs and the separation of their components. Figure 30 presents the distribution of wide catalogue pairs according to the unbiassed estimator f_c, calculated according to (2.19). These data do not show the expected distribution. Including the earlier limitation (f < 100) used to segregate false systems we have for the wide pairs <f_c> = 12.7 ± 3.4 over the range [100 - 260] kpc. This value is only slightly higher than the mean for the entire sample of double systems. Estimates for the orbital mass for wide pairs are more sensitive to errors in the velocity measurements. If one takes this into account by incorporating absolute errors in the radial velocity difference that are increased by a factor of 1.4 (Karachentsev, 1983) this correction reduces <f_c> to a value of 5.2 ± 3.6.

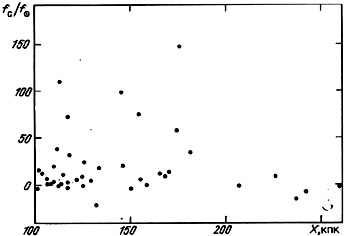Figure 30.

The existence of an extended halo around double galaxies should also reveal itself through an apparent correlation of the factor µ = M / (M₁ + M₂) with the separation. The distribution of 119 pairs in a (logµ, log X) diagram (figure 31) does not show the expected correlation. Pairs with µ below the critical value 64 / 3, shown by a dashed line, are randomly distributed in the lower part of the diagram. In the region X > 10 kpc one may note the presence of false pairs all over the region below the dashed line. One could suppose that all pairs with values of µ exceeding the critical value have massive haloes but, as we already noted, the apparent number of such systems (21%) is barely half of the expected number of false double systems in the sub-sample we examined.

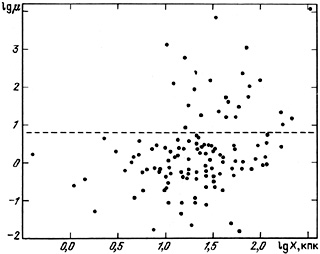Figure 31.

Van Moorsel (1983) proposed verifying the presence of massive spherical haloes around double galaxies using the following simple argument. Take flat rotation curves for pair components with amplitudes V_m1 and V_m2 extending to the contact point of both haloes. If the radius of these haloes is taken as r₁₂/2, where r₁₂ is the spatial separation between components, then the total mass of members of the pair will be M₁ = G^-1(r₁₂ / 2)V²_m1 and M₂ = G^-1(r₁₂ / 2)V²_m2. Incorporating the effective velocity of rotation of the galaxy we have

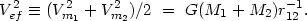For circular motions the expression simplifies to y² V₁₂² cos² = G(M₁ + M₂) r₁₂^-1 cos² where V₁₂ and y are respectively the difference in spatial velocity and projected radial velocity of the components and is the angle between the line of sight and the relative velocity vector of the galaxies. Therefore, the combination of observed quantities

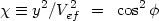(4.43)

depends only on the angle . For random orientations of pairs p() = sin, from which it follows that the observed quantity has the distribution

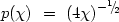(4.44)

in the interval [0 1], with mean value = 1/3.

We calculated the values of for 84 double galaxies for which measurements of V_m are available either from the rotation curve or from the line width W₂₀ (Karachentsev, 1985). The observed distribution for these double galaxies is shown as the histogram in figure 32. The curve indicates the expected distribution (4.44). As is apparent the hypothesis about contiguous massive haloes around galaxies in pairs does not agree with the observational data to the desired extent. NOTE: Do we really see the same thing here ? A significant fraction of the double systems (25%) are found in the forbidden region > 1, which cannot be explained solely by errors in radial velocity measurements. By analogy with the data of figure 29 one might hope that a better agreement of the observed distribution with the predicted form would be obtained for pairs that have elliptical motion. However, galaxies with massive extended haloes and strongly plunging orbits should merge rapidly because of their mutual dynamical interaction.

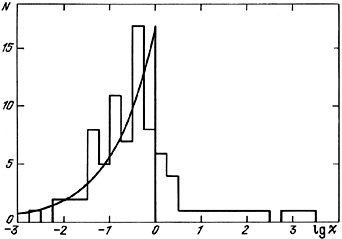Figure 32.

For these reasons the hypothesis of extended haloes around double galaxies does not yield a satisfactory description of the observational data. Analysing individual cases with large values of µ or we note that such pairs are generally associated with the known clusters Perseus, Coma, or Hercules. In such supercluster regions there is an especially high probability of observing close so-called pairs of galaxies along the line of sight with velocity differences in the range 300 to 1000 km/s at true separations of several megaparsecs. For example, for pair number 27 with radial velocities 1841 km/s and 11352 km/s Rubin and Ford (1987) showed that the amplitude of the rotation curve and the luminosity of each galaxy could be explained only under the assumption that their distance from the observer agrees with that indicated by the radial velocity of each galaxy. Extending such criteria to other pairs with large radial velocity differences also suggests that they are chance superpositions of galaxies along the line of sight.

Independent information on the environments of non-isolated pairs with large orbital mass-to-luminosity ratios may be obtained by examining the galaxies from the CGCG around such pairs. This examination shows a marked excess in the numbers of neighbour galaxies by comparison to a Poisson distribution over characteristic scales less than 200 kpc. For selected pairs, such as numbers 127, 190, 263, 416, 548 and 584, where radial velocities are also known for the surrounding galaxies, their velocities are close to the radial velocities of the associated pair members.

The association of pairs with larger systems of galaxies is clearly demonstrated by the data in table 10, which presents the 12 nearest double galaxies, along with their mean radial velocity, distance from the observer and membership in galaxy groups according to de Vaucouleurs (1975). As we see, with the exception of a single pair, all of these belong to the closest groups of galaxies. We may conclude from this that such pairs as number 379 = M51 are in fact gravitationally bound sub-structures in groups. However, in several cases (such as number 218 = M81 + M82) the isolation of the pairs and the correctness of their orbital mass estimates may be somewhat doubtful. Similar situations may also be characterized for more distant double galaxies, but the possibility of identifying their membership in groups and clusters is limited by the paucity of data on radial velocities. Comparisons of this kind illustrating the role of false non-isolated pairs on estimates of the mean orbital mass-to-luminosity ratio have been presented in the articles by Karachentsev and Fesenko (1979), Karachentsev (1980b), Fesenko (1981), van Moorsel (1983), and White et al. (1983).

Blackman and van Moorsel (1984) performed photometry on the members of 13 pairs with rotation curves measured in the 21-cm radio line, including three pairs satisfying the isolation criteria of our catalogue. They showed that for 10 components the mass-to-luminosity ratio remains constant along the galactic radius while for the other 16 it rises from the center to the periphery. The mean integrated M/L ratio for 26 galaxies is 6.4 ± 0.8 for H = 75 km/s/Mpc.

Karachentsev and Mineva (1984b) found a ratio close to the present value <M(R₂₅) / L> = 6.2 ± 0.7 for 37 double galaxies with measured rotation curves. They also noticed that the components of double systems are not distinguished from single galaxies either in mean mass-to-luminosity ratio or in the fraction possessing flat rotation curves (~ 80%). For 13 pairs with measured mass for both components, the mean ratio of orbital mass to the sum of the individual masses <µ> = 1.02 ± 0.32. Grouping the double galaxies by type of rotation curves (flat or Keplerian) made no difference to <µ>, within the statistical errors. The mean projected separation on the sky between members of the 13 pairs exceeded the sum of their standard radii by a factor of 2.0 ± 0.3. These results show that there is no evidence for an excess of mass in double systems on scales greater than ~ 2R₂₅.

We do not wish to appear to have solved the question of the nature of hypothetical haloes around double galaxies, because we do not see this as appropriate at this point. We will limit ourselves to a few remarks. In models of the Universe where the largest contribution to the cosmological parameter ₀ is from neutrinos with non-zero mass, a marked concentration of dark mass (neutrinos) should form around the potential wells of systems of galaxies (Doroshkevich, 1984). One would expect that this would also occur in double systems. To check this proposition we examined the evidence for excess orbital mass over the sum of the individual masses for pair members, but no evidence for a correlation between these quantities appeared.

In summary, analysis of orbital mass estimates for a uniform sample of 585 double galaxies leads us to the following conclusions about the dynamical properties of these most simple systems of galaxies.

1. The apparent magnitude or angular diameter of the galaxies exhibits a weak dependence on their distance from the observer. For the objective isolation criteria basic to our catalogue, a significant number of false double systems appears, foremost among them the very brightest members of groups and clusters of galaxies. A similar situation occurs in the samples of double galaxies of Turner (1976a) and Peterson (1979a), where much weaker isolation criteria were applied. This, along with proper accounting for the presence of false pairs, accounts for the significant differences in estimates of the mean orbital mass among these authors. Excluding from our catalogue 98 projected non-isolated pairs (which number is a factor of two less than that expected from these criteria, based on Monte Carlo simulations) reduces the mean estimate of orbital mass and brings it into agreement with typical values of the mass of galaxies derived from their rotation.

2. After accounting for orientation factors and errors in radial velocity measurement we show that the ratio of orbital mass to the sum of luminosities in pairs has a distribution in the interval 0 to 30 with mean value 7.8 ± 0.7 f and standard deviation 6.5. The form of this distribution does not contradict the log-normal distribution of individual estimates of M/L characteristic of individual galaxies.

3. With these observations it is possible to limit the possible types of orbital motion of galaxies in pairs. Considering three different tests for orbital shapes, we conclude that the motion of galaxies in pairs is close to circular. From these data we find the best agreement for a typical eccentricity of e = 0.25.

4. Comparing the orbital mass of double galaxies with the sum of their individual mass, determined from rotation curves, 21-cm line widths, or the velocity dispersion of stars in the simple parts of the component galaxies, we show that practically all of the mass is located within their standard optical radii, R₂₅. This allows one with some confidence to describe the dynamics of double galaxies in a Keplerian manner.

5. Wide pairs of galaxies with a separation between components X > 100 kpc have in the mean exactly the same ratio of orbital mass to luminosity as do tight, compact pairs. The ratio of orbital mass to the sum of the individual mass of their components also does not exhibit any dependence on the separation X. These results argue against the existence of extended haloes of invisible matter around double galaxies.