5. CHAPTER 5. STRUCTURAL PROPERTIES OF DOUBLE GALAXIES

5.1. Morphological Types and Masses of Double Galaxies

In the preceding chapters we have viewed galaxies in pairs as elementary units, ignoring any differences of morphological type. By taking these differences into account we can find new laws concerning the origin and coupled evolution of double galaxies. The first version of the catalogue of pairs (Karachentsev, 1972) incorporated only broad divisions of double galaxies into ellipticals and spirals. In the present version of the catalogue (Appendix 1), we extend this to a more detailed structural classification of galaxies by Hubble type: E, S0, Sa, Sb, Sc, Sm (see section 2.4). The morphological types are based largely on high contrast prints. For a small fraction of the cases, about 20%, we also had large scale plates taken by the author. In determining types, we further considered estimates of their colours from comparison of the blue and red Palomar charts.

Morphological classification of faint galaxies on the Palomar charts is often rather uncertain because of the high contrast and overexposure of the central regions of galaxies, which applies particularly to objects of low surface brightness. A further difficulty arises for tight pairs, where the classical indicators of morphological type are strongly disturbed by the effects of interaction. To estimate the errors in classification we turn to the data by Eichendorf and Reinhart (1981), who compiled a sample of double galaxies which satisfy any of the criteria of Holmberg (1937), Karachentsev (1972) or Turner (1976a). For their sample they collected data on the apparent axial ratio, position angles and morphological type (E, S0, Sa, Sb, Sc, Irr) for 1105 pairs of galaxies. The distribution by Hubble type of 323 galaxies in common between our catalogue (K) and the sample of Eichendorf and Reinhart (ER) is presented in Table 11, from which we can draw some conclusions. The fractional number with identical classification (the sum of the diagonal elements of the matrix) is 41%. The number of cases with errors of one and two classes are respectively 41% and 13%. The number of galaxies for which the difference in type Ty 3 does not exceed 5%. The mean quadratic error in determining the Hubble type is < Ty²>^1/2 = 1.18, with a mean value <Ty^K - Ty^ER> = - 0.8 ± 0.07, showing that any classification errors are not large ⁽⁴⁾. Know, however, that this comparison was performed on a selection of bright objects, for which the structural types may be determined with more certainty than for galaxies closer to the catalogue limit.

Table 12 shows how the pairs in the catalogue are distributed by morphological types of the brighter and fainter components. Here and in what follows we will discuss only those pairs for which the orbital mass-to-luminosity ratio does not exceed 100 f. It follows from these data that there is no large difference between the structural types of the bright and faint components. The galaxies of a given Hubble class (excluding Sm) have an excellent chance of being either the brighter or the fainter member of a double system. The main property of this matrix of morphological types is the excess number of pairs along its diagonal. The tendency of galaxies located in pairs to share morphological types was remarked by Karachentsev and Karachentseva (1974) and confirmed by Noerdlinger (1979). To estimate the magnitude of this effect, if _i is the relative number of Hubble type i, (i = 1, 2, ..., 6) in a sub-sample of double galaxies, then the probability of encountering two galaxies in a double system with types i and j is given by the relative fraction _ij = 2_{i j} (i j) and _ii = _i². The observed and expected number of pairs are presented in matrix form in Table 13. As we see, double galaxies with the same structural type are encountered in the catalogue significantly more often than expected by chance. This excess even occurs for pairs with mixed Hubble types. Comparison of these two distributions using a ² criterion shows that the assumption of random distributions of morphological types may be ruled out at the level p << 10^-4. The largest effect is seen for galaxies at the extremes of the Hubble sequence, Sm and E.

It is well known that the distributions of elliptical and spiral galaxies are coupled strongly to the local concentration of galaxies. Objects of early type, E and S0, concentrate in the central regions of rich clusters, while spirals and irregular galaxies are distributed on the edges of clusters, in smaller groups and throughout extra-galactic space. This universal law is just as visible in the simplest systems, the double galaxies. Table 14 presents the number n_i and relative fraction _i of various Hubble types among catalogue double galaxies and single (isolated) galaxies from the Karachentseva (1973) catalogue. Also shown is a sub-sample of wide pairs in which the components have a projected mutual separation exceeding 50 kpc. It is apparent that the late types (Sb, Sc, Sm) are encountered less often among double galaxies than among isolated systems. This conclusion is supported by the statistics for the axial ratios of spiral galaxies in both catalogues (Karachentsev and Karachentseva, 1974), as well as by radio data on the abundance of neutral hydrogen (Balkowski and Chamaraux, 1981). Note that the photometric limits in the region of the sky covered by the catalogues of pairs and of isolated galaxies are identical, and so, therefore, differences in the occurrence of early and late types cannot be artefacts of any sort of selection effects.

In the literature one may encounter additional discussions about the dependence of the structural type of a galaxy on that of its nearest neighbour. One source of such an effect might be the heating of the disk of a spiral galaxy due to the passage of massive satellites. Numerical experiments by Gerhard and Fall (1983) show, however, that `blowing up' a galaxy (increasing the stellar velocities in the z coordinate) is effective only when the velocity of relative motion of the two galaxies is more than three times the mean rotation velocity of the disk. This condition is satisfied in rich clusters, but in pairs and small groups this method is not sufficient to change the thin disk of a spiral into a thick one. Dressler (1980) examined a further mechanism for morphological segregations, according to which the formation of gaseous disks in spiral galaxies, and stellar sub-systems within the disks, takes place over a time t 2 × 10⁹ years. If galaxies have close neighbours during this period, then their presence may block or delay the formation of flat sub-systems.

We now return to the question of the correlation of structural types between galaxies in pairs. Let n₀( Ty) indicate the total observed number of double systems in the catalogue with Hubble type difference Ty = 0, 1, ...5, and let n_p( Ty) be the analogous expected number of systems for a random distribution of galaxies in pairs. These numbers are easily derived from the diagonal elements of the matrix in table 13. We introduce the correlation function by morphological type,

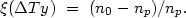(5.1)

The values of this function for the sample of 487 pairs are presented in figure 33 as diamonds, the height of which indicates the statistical standard deviation in the mean. The data for 118 wide pairs are indicated by the points, with their associated standard deviation. NOTE: We will have to include the more recent Japanese work on nearest neighbours, incorporating radial velocities, at this point.

Figure 33.

We note here two circumstances. According to the data in figure 33 the correlation function ( Ty) is significant only for Ty 1. For a mean error in the type (Ty) 1, the error in classification should contribute significantly to the correlation function. Detailed estimates show that this will increase the amplitude of (0) by 1.5 to 2 times.

These estimates of the probability of encountering galaxies of various morphological types in double systems characterize their catalogue, and not their spatial, distribution. This caution applies as well to the correlation function for Hubble types. The difference between the partial distributions of objects of two types, per unit volume and in the catalogue, depends on the difference in their luminosity functions. An attempt to go from the catalogue to the true distribution of galaxies by morphological type was made by Arakelian (1983b).

Table 15 illustrates the variation along the Hubble sequence of the mean absolute magnitude and mean linear diameter of double galaxies, along with the standard deviations of these quantities, (M) and (A). Excluding the irregular galaxies, the luminosity function and diameter function for pair members does not depend strongly on morphological type, in agreement with the results of Sandage et al. (1985). Because the luminosity of Sm galaxies is an order of magnitude lower than for other types, the true density of such objects per unit volume will be considerably higher than in the catalogue (magnitude limited) sample. Thus Sm galaxies comprise 45% of the 12 closest pairs (table 10), instead of the 6% characteristic of the entire catalogue.

We have already remarked that pairs of galaxies exhibit a morphological segregation which depends on separation. In Table 16 we present the mean values of the projected separation and radial velocity difference for double galaxies of various types. On passing from early to late Hubble types we note a tendency for increasing separation and decreasing radial velocity difference. However, double systems containing dwarf components of type Sm deviate from this property, due to selection effects (the criteria discriminate against wide pairs containing galaxies of low luminosity).

In the previous chapter we concluded that the orbital masses of double galaxies agreed very well with their individual masses measured from rotation curves. Do we observe such agreement for selected morphological types of galaxies ? The data on this question have a somewhat contradictory history. Page (1952, 1960, 1961), who first measured radial velocities for double galaxies, gave estimates for orbital mass-to-luminosity ratios for elliptical galaxies two orders of magnitude greater than for spirals. Page considered that this result indicated the large virial values of f in clusters, in which elliptical and lenticular systems are concentrated. On the other hand, a strong difference between EE and SS galaxies by mass-to-luminosity ratio is not supported by measures of the stellar velocity dispersion in the central parts of elliptical galaxies. These results may be satisfied by the simple proposition that ellipticals concentrated in rich clusters and compact groups should include a significant number of false pairs where the galaxies are projected nearly in contact with one another and have radial velocity differences of order the virial velocity of the cluster. Further, excluding the false pairs by means of the isolation criterion, we may consider the ratio f_E/f_S. Using the sub-samples of Turner (1976b), Karachentsev (1977), and Peterson (1979b) this ratio is reduced to f_E / f_S 2. We now examine the dependence of f (Ty) on the properties of pairs for the entire sample catalogue.

The estimates in the literature on the mass-to-luminosity ratio for systems of various types are collected in table 17. The first column indicates the Hubble type of the galaxies, the second, the mean mass-to-luminosity ratio <f> and the standard deviation in the mean, the third indicates the number of observed objects n, and the final one the source for the data. The data as presented by various authors have been reduced to a standard system of apparent magnitude B_T⁰ and standard radius R₂₅ for a Hubble constant H = 75 km/s/Mpc and an absolute solar magnitude M = 5.40. Within the bounds of each morphological type, the mass-to-luminosity ratios as obtained by various methods (stellar velocity dispersion, rotation curve, or 21-cm HI line width) showed satisfactory agreement. For galaxies of type Sm estimates of the mass from the 21-cm profile may be affected by systematic errors in measuring the width of weak lines and by neglect of turbulent velocities in the objects seen almost face-on (Lewis, 1983).

The compilation of these data supports the general trend remarked by Faber and Gallagher (1979): with decreasing importance of the spheroidal component to the integrated luminosity of the galaxy, the mass-to-luminosity ratio decreases from values f (E) 10 to f (Sm) 4. An analogous trend can be demonstrated for the mean ratio of orbital mass to luminosity for double galaxies. Of the 487 pairs having f < 100 we have selected the systems with identical structural types of the components. To reduce the role of radial velocity errors we excluded 15 pairs for which the error f_u (see section 4.2) exceeds 5. Averaging the orbital mass-to-luminosity ratios gives the results shown in the last column of table 15. Because of an unsatisfactorily small sample size, there was only one S0+S0 pair, so the mean for this type was calculated by including the 14 E+S0 pairs.

The reduced data are presented together in figure 34. The mean orbital mass-to-luminosity ratio for 107 pairs is shown as diamonds, the height of which indicates the standard deviation of the mean. The points show the mean for various types of galaxies according to the data in table 17. The mean individual mass-to-luminosity ratios for 209 individual components (Karachentsev, 1985) are shown as the crosses.

Figure 34.

In agreement with the conclusions of the previous chapter, we may confidently assert that the orbital mass-to-luminosity ratio for double galaxies agrees with the individual f values not only in general but also for each individual morphological type. The contention often found in the literature that the masses of pairs of elliptical (Rood, 1976) and of dwarf (Lake and Schommer, 1984) galaxies are unusually high (f 100) are contradicted by the results in figure 34. The excessive estimates of pair masses by these authors are apparently due to the inclusion of a large number of false double systems. It must be stressed that the excellent agreement between orbital and individual masses for galaxies of every Hubble type would be very difficult to understand if the majority of the mass of double galaxies were located in invisible extensive haloes around the individual components of double systems.

⁴ For 76 galaxies in common with the catalogue of de Vaucouleurs et al. (1976) (V) we find <Ty^K - Ty^V> = -0.16 ± 0.10 and < Ty² >^1/2 = 0.87. Back.