6.4. Peculiar Motions of Pairs

In section 3.3 we showed that the distribution of the absolute radial velocity difference in isolated double systems is well fit by an exponential with a mean of 120 km/s and rms value <y²>^1/2 = 2^1/2<y> = 170 km/s. These values show indisputable evidence for false pairs in the sample and for the role of radial velocity measurement errors.

Large surveys of galaxy redshifts to fixed limiting magnitudes allow one to determine the value of <y²>^1/2 without basing it on individual pairs. Thus, Davis et al. (1978) from radial velocity differences for nearest neighbour galaxies brighter than 13th magnitude found a value <y²>^1/2 = 300 ± 30 km/s. A much higher value, 450 ± 100 km/s, was found by Kirshner et al. (1978) using analogous measurements for galaxies brighter than 15th magnitude in separate square regions. Bean et al. (1983) observed 300 galaxies brighter than 17th magnitude and found <y²>^1/2 = 250 ± 50 km/s. This agrees with galaxies for which the projected separation does not exceed 5 Mpc. All of these estimates, to their various respective limits, must be over-estimates because they include members of groups and clusters with large virial motions. This difficulty was treated by Rivolo and Yahil (1981) who found for bright galaxies with X < 500 kpc the value <y²>^1/2 = 100 ± 15 km/s. According to Davis and Peebles (1983) the rms velocity difference depends only weakly on separation (~ X^0.13) and is 194 km/s for X < 130 kpc. This last estimate is based on the analysis of the largest sample of galaxies yet presented and is in excellent agreement with the value of <y²>^1/2 for isolated pairs in our catalogue.

Besides the rms velocity for orbital motion of double galaxies, it is important to know as well the rms peculiar (chaotic) velocity (V_p) of the centers of the pairs with respect to co-moving cosmological coordinates. Entropy, adiabatic, and other theories of the development of large-scale structures in the Universe lead to quite different values for such chaotic velocities, from ~ 2 to ~ 800 km/s. Therefore, observational determination of (V_p) might distinguish among various scenarios for the origin of double systems. The most concrete relevant data are in Turner et al. (1979), which presents the results of numerical modelling of the gravitational clumping of galaxies into systems of various multiplicities. Table 3 of Turner et al. presents the values of the orbital and chaotic motions of the model pairs projected along the line of sight. The calculations were performed for two values of the cosmological density parameter, ₀ = 1 and ₀ = 0.1. If one excludes the double systems with large radial velocity differences (y > 1000 km/s), then for the ₀ = 1 model Turner et al. (1979) give <y²>^1/2 = 390 km/s and (V_p) = 483 km/s. The model with a low value of the density parameter, ₀ = 0.1, has a much lower temperature for the galactic `gas': <y²>^1/2 = 230 km/s and (V_p) = 132 km/s. In the straightforward picture of gravitational clustering these parameters both in themselves and in the form of the dimensionless ratio (V_p) / <y²>^1/2 may serve as sensitive indicators of the mean cosmological density, ₀.

To determine the magnitude of peculiar motions of the centers of pairs we took the data of table 10, which shows the mean velocities of the centers of pairs and their distance D from the de Vaucouleurs groups (1975) which contained these pairs. The distribution of 11 pairs in separation and mean velocity, taking into account the individual component luminosities, is shown as the filled points in figure 46. The scatter about a linear Hubble flow gives (V_p) = 115 km/s. Note that the dispersion of pairs in this diagram grows with increasing distance from the observer. Such an effect generally arises from significant errors in the distance estimates, and if one takes this into account then the value for peculiar motions of the centers drops to 80 km/s ⁽¹⁰⁾ . As a control we have also used estimates of the individual distance modulus for double galaxies from Bottinelli et al. (1984, 1985), using 21-cm HI line widths. These are shown with plus signs in figure 46. The dispersion of these data with respect to the mean (dashed line) is rather high due to inaccuracies in the estimates of D. The formal value for the peculiar velocity is 220 km/s.

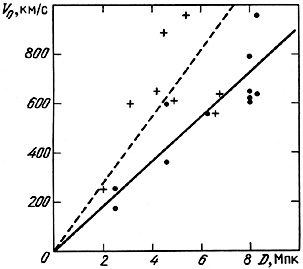Figure 46.

These calculations of the chaotic motion for pair centers did not take into account the fact that nearly all nearby double galaxies are also members of the de Vaucouleurs groups which themselves have virial velocity dispersions ~ 100 km/s. Therefore, the peculiar velocities of the pair centers relative to a co-moving coordinate system may be wholly due to motions driven by the potential within the corresponding groups and clusters. Though the observational data are still sparse, we may conclude that the typical random velocities of pair centers are not higher than the mean relative motion of their components, i.e., (V_p) <y²>^1/2. This is in accord with the model results presented by Turner et al. (1979) which suggest that the gravitational clustering of galaxies indicates a mean mass density for the Universe an order of magnitude lower than the critical density.

To review this chapter briefly, we have examined the general characteristics of double galaxies as an extragalactic population. Three independent ways of estimating the relative number of galaxies in double systems were discussed. The frequency of double galaxies per unit volume is considerably higher than the fraction of objects in the catalogue (0.042), and reaches = 0.12 ± 0.02. The spatial distribution of pairs follows the general trend of hierarchical clustering of galaxies in systems of various multiplicities and scales. All (or almost all) nearby pairs are also members of known nearby de Vaucouleurs groups. About half of the pairs with V₀ < 2500 km/s fall within the Local Supercluster of galaxies.

Pairs of galaxies in groups and clusters are distinguished by a small separation between components. Within systems, pairs exhibit a marked tendency to occur in the regions of lower density surrounding clusters, relative to the distribution of single members. Treating this as a result of the tidal disruption of wide pairs gives tidal mass estimates for the systems which agree well with the virial mass estimates.

The two-point correlation function for the centers of pairs in the interval [0.7 - 20] Mpc has a systematically greater amplitude than the standard Peebles function for ordinary galaxies. The maximum difference between them occurs on a scale ~10 Mpc, which may be explained by the relative excess of double systems on the boundaries of superclusters.

The rms velocity difference for components of double systems is 170 km/s. Very nearly this value (194 km/s), is given by the radial velocity differences for galaxy nearest neighbours on the sky, in surveys to a fixed limiting magnitude. From the scatter in the velocity/separation diagram we estimated the peculiar velocities of pair centers to be (V_p) 100 km/s, which agrees approximately with the virial motions in groups. Small values of the chaotic velocity for pair centers agree with the results of the modelling of gravitational clustering of galaxies (Turner et al., 1979) for a mean mass density of the Universe of order one tenth the critical value.

¹⁰ A very similar estimate of the peculiar motions along the line of sight, (70 ± 40) km/s, was found by Tsvetkov (1981) for field galaxies with distances D < 20 Mpc. Back.