Annu. Rev. Astron. Astrophys. 1998. 36: 189-231 Copyright © 1998 by Annual Reviews. All rights reserved

5.3. Physical Regulation of Star Formation Rate

Although star-forming galaxies span millionfold ranges in their present SFRs and physical conditions, there is a remarkable continuity in some of their properties, and these relationships provide important insights into the physical regulation of the SFR over this entire spectrum of activities.

We have already seen evidence from Figures 5 and 7 that the global SFRs of disks and nuclear starbursts are correlated with the local gas density, though over very different ranges in density and SFR per unit area. The left panel of Figure 9 shows both sets of data plotted on a common scale, and it reveals that the entire range of activities, spanning 5-6 orders of magnitude in gas and SFR densities, fits on a common power law with index N ~ 1.4 (Kennicutt 1998). The SFRs for the two sets of data were derived using separate methods (H luminosities for the normal disks and FIR luminosities for the starbursts), and to verify that they are measured on a self-consistent scale, Figure 9 also shows H-derived SFR gas densities for the centers (1-2 kpc) of the normal disks (plotted as open circles). The tight relation shows that a simple Schmidt (1959) power law provides an excellent empirical parametrization of the SFR, across an enormous range of SFRs, and it suggests that the gas density is the primary determinant of the SFR on these scales.

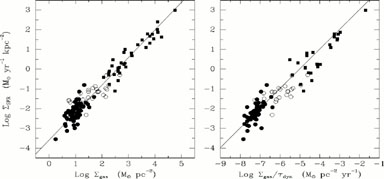Figure 9. (Left) The global Schmidt law in galaxies. Solid points denote the normal spirals in Figure 5, squares denote the circumnuclear starbursts in Figure 7. The open circles show the SFRs and gas densities of the central regions of the normal disks. (Right) The same SFR data but plotted against the ratio of the gas density to the average orbital time in the disk. Both plots are adapted from Kennicutt (1998).

The uncertainty in the slope of the best-fitting Schmidt law is dominated by systematic errors in the SFRs, with the largest being the FIR-derived SFRs and CO-derived gas densities in the starburst galaxies. Changing either scale individually by a factor of two introduces a change of 0.1 in the fitted value of N, and this is a reasonable estimate of the systematic errors involved (Kennicutt 1998). Incorporating these uncertainties yields the following relation for the best-fitting Schmidt law:

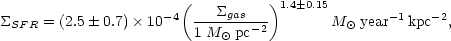(7)

where _SFR and _gas are the disk-averaged SFR and gas surface densities, respectively.

As discussed by Larson (1992), Elmegreen (1994), a large-scale Schmidt law with index N ~ 1.5 would be expected for self-gravitating disks if the SFR scales as the ratio of the gas density () to the free-fall time scale ( ^-0.5) and the average gas scale height is roughly constant across the sample ( ). In a variant on this picture, Elmegreen (1997), Silk (1997) have suggested that the SFR might scale with the ratio of the gas density to the average orbital time scale; this is equivalent to postulating that disks process a fixed fraction of their gas into stars in each orbit around the galactic center. The right panel of Figure 9, also adapted from Kennicutt (1998), shows the correlation between the SFR density and _gas / _dyn for the same galaxies and starbursts. For this purpose _dyn is defined as one disk orbit time, measured at half of the outer radius of the star-forming disk, in units of years (see Kennicutt 1998 for details). The line is a median fit to the normal disks with slope contrained to unity, as predicted by the simple Silk model. This alternative "recipe" for the SFR provides a fit that is nearly as good as the Schmidt law. The equation of the fit is

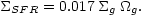(8)

In this parametrization, the SFR is simply ~ 10% of the available gas mass per orbit.

These parametrizations offer two distinct interpretations of the high SFRs in the centers of luminous starburst galaxies. In the context of the Schmidt law picture, the star formation efficiency scales as _g^{(N - 1)}, or _g^0.4 for the observed relation in Figure 9. The central starbursts have densities that are on the order of 100-10,000 times higher than in the extended star-forming disks of spirals, so the global star formation efficiencies should be 6-40 times higher. Alternatively, in the kinematic picture, the higher efficiencies in the circumnuclear starbursts are simply a consequence of the shorter orbital time scales in the galaxy centers, independent of the gas density. Whether the observed Schmidt law is a consequence of the shorter dynamical times or vice versa cannot be ascertained from these data alone, but either description provides an excellent empirical description or "recipe" for the observed SFRs.

These simple pictures can account for the high SFRs in the starburst galaxies, as well as for the observed radial variation of SFRs within star-forming disks (Kennicutt 1989, 1998). However the relatively shallow N ~ 1.4 Schmidt law cannot account for the strong changes in disk SFRs observed across the Hubble sequence if the disks evolved as nearly closed systems (Kennicutt et al 1994). Likewise, the modest changes in galaxy rotation curves with Hubble type are too small to account for the large differences in star formation histories with a kinematical model such as in Equation 8. The explanation probably involves star formation thresholds in the gas-poor galaxies (Kennicutt 1989, 1997), but the scenario has not been tested quantitatively, and it is possible that other mechanisms, such as infall of gas, merger history, or bulge-disk interactions are responsible for the strong changes in star formation histories across the spiral sequence.