All of modern cosmology stems essentially from an application of the Copernican principle: we are not at the center of the universe. In fact, today we take Copernicus' idea one step further and assert the "cosmological principle": nobody is at the center of the universe. The cosmos, viewed from any point, looks the same as when viewed from any other point. This, like other symmetry principles more directly familiar to particle physicists, turns out to be an immensely powerful idea. In particular, it leads to the apparently inescapable conclusion that the universe has a finite age. There was a beginning of time.
We wish to express the cosmological principle mathematically, as a symmetry. To do this, and to understand the rest of these lectures, we need to talk about metric tensors and General Relativity, at least briefly. A metric on a space is simply a generalization of Pythagoras' theorem for the distance ds between two points separated by distances dx = (dx, dy, dz),
 |
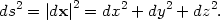(1) |
We can write this as a matrix equation,
 |
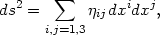(2) |
where
i j
is just the unit matrix,
 |
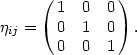(3) |
The matrix
i j
is referred to as the metric of the space, in this case
a three-dimensional Euclidean space. One can define other, non-Euclidean
spaces by specifying
a different metric. A familiar one is the four-dimensional "Minkowski"
space of special relativity, where the proper distance between two
points in spacetime is given by
 |
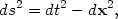(4) |
corresponding to a metric tensor with indices
µ, 
= 0,..., 3:
 |
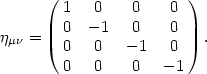(5) |
In a Minkowski space, photons travel on null paths, or geodesics, ds2 = 0, and massive particles travel on timelike geodesics, ds2 > 0. Note that in both of the examples given above, the metric is time-independent, describing a static space. In General Relativity, the metric becomes a dynamic object, and can in general depend on time and space. The fundamental equation of general relativity is the Einstein field equation,
 |
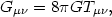(6) |
where
Tµ is a
stress energy tensor describing the distribution of mass in
space, G is Newton's gravitational constant and the Einstein Tensor
Gµ is a
complicated function of the metric and its first
and second derivatives. This should be familiar to anyone who has taken
a course in
electromagnetism, since we can write Maxwell's equations in matrix form as
 |
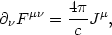(7) |
where
Fµ is
the field tensor and Jµ is the current. Here we
use the standard
convention that we sum over the repeated indices of four-dimensional
spacetime = 0, 3.
Note the similarity
between Eq. (6) and Eq. (7). The similarity is more than formal: both have a
charge on the right hand side acting as a source for a field on the left
hand side. In the
case of Maxwell's equations, the source is electric charge and the field
is the electromagnetic
field. In the case of Einstein's equations, the source is mass/energy,
and the field is
the shape of the spacetime, or the metric. An additional feature of the
Einstein field equation
is that it is much more complicated than Maxwell's equations:
Eq. (6) represents
six independent nonlinear partial differential equations of ten
functions, the components of the (symmetric) metric tensor
gµ(t, x). (The other four degrees of
freedom are accounted for by invariance under transformations among the
four coordinates.)
Clearly, finding a general solution to a set of equations as complex as the Einstein field equations is a hopeless task. Therefore, we do what any good physicist does when faced with an impossible problem: we introduce a symmetry to make the problem simpler. The three simplest symmetries we can apply to the Einstein field equations are: (1) vacuum, (2) spherical symmetry, and (3) homogeneity and isotropy. Each of these symmetries is useful (and should be familiar). The assumption of vacuum is just the case where there's no matter at all:
 |
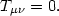(8) |
In this case, the Einstein field equation reduces to a wave equation,
and the solution is gravitational radiation. If we assume that the
matter distribution
Tµ has
spherical symmetry, the solution to the Einstein field equations is the
Schwarzschild
solution describing a black hole. The third case, homogeneity and
isotropy, is the one
we will concern ourselves with in more detail here
[1]. By
homogeneity, we mean that the
universe is invariant under spatial translations, and by isotropy we
mean that the universe
is invariant under rotations. (A universe that is isotropic everywhere
is necessarily
homogeneous, but a homogeneous universe need not be isotropic: imagine a
homogeneous space
filled with a uniform electric field!) We will model the contents of the
universe as a perfect fluid with density
and pressure
p, for which the stress-energy tensor is
 |
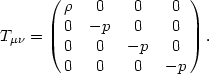(9) |
While this is certainly a poor description of the contents of the universe on small scales, such as the size of people or planets or even galaxies, it is an excellent approximation if we average over extremely large scales in the universe, for which the matter is known observationally to be very smoothly distributed. If the matter in the universe is homogeneous and isotropic, then the metric tensor must also obey the symmetry. The most general line element consistent with homogeneity and isotropy is
 |
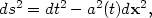(10) |
where the scale factor a(t) contains all the dynamics of the universe, and the vector product dx2 contains the geometry of the space, which can be either Euclidian (dx2 = dx2 + dy2 + dz2) or positively or negatively curved. The metric tensor for the Euclidean case is particularly simple,
 |
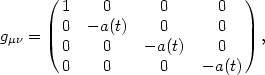(11) |
which can be compared to the Minkowski metric (5). In this Friedmann-Robertson-Walker (FRW) space, spatial distances are multiplied by a dynamical factor a(t) that describes the expansion (or contraction) of the spacetime. With the general metric (10), the Einstein field equations take on a particularly simple form,
 |
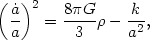(12) |
where k is a constant that describes the curvature of the space: k = 0 (flat), or k = ±1 (positive or negative curvature). This is known as the Friedmann equation. In addition, we have a second-order equation
 |
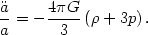(13) |
Note that the second derivative of the scale factor depends on the
equation of state
of the fluid. The equation of state is frequently given by a parameter
w, or
p = w. Note that for any fluid with positive pressure, w
> 0, the expansion of
the universe is gradually decelerating,
< 0: the mutual
gravitational attraction
of the matter in the universe slows the expansion. This characteristic
will be central to the discussion that follows.