2.2. Einstein's "greatest blunder"

General relativity combined with homogeneity and isotropy leads to a startling conclusion: spacetime is dynamic. The universe is not static, but is bound to be either expanding or contracting. In the early 1900's, Einstein applied general relativity to the homogeneous and isotropic case, and upon seeing the consequences, decided that the answer had to be wrong. Since the universe was obviously static, the equations had to be fixed. Einstein's method for fixing the equations involved the evolution of the density with expansion. Returning to our analogy between General Relativity and electromagnetism, we remember that Maxwell's equations (7) do not completely specify the behavior of a system of charges and fields. In order to close the system of equations, we need to add the conservation of charge,

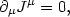(14)

or, in vector notation,

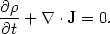(15)

The general relativistic equivalent to charge conservation is stress-energy conservation,

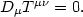(16)

For a homogeneous fluid with the stress-energy given by Eq. (9), stress-energy conservation takes the form of the continuity equation,

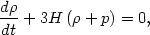(17)

where H = / a is the Hubble parameter from Eq. (12). This equation relates the evolution of the energy density to its equation of state p = w . Suppose we have a box whose dimensions are expanding along with the universe, so that the volume of the box is proportional to the cube of the scale factor, V a³, and we fill it with some kind of matter or radiation. For example, ordinary matter in a box of volume V has an energy density inversely proportional to the volume of the box, V^-1 a^-3. It is straightforward to show using the continuity equation that this corresponds to zero pressure, p = 0. Relativistic particles such as photons have energy density that goes as V^-4/3 a^-4, which corresponds to equation of state p = / 3.

Einstein noticed that if we take the stress-energy T_µ and add a constant , the conservation equation (16) is unchanged:

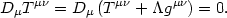(18)

In our analogy with electromagnetism, this is like adding a constant to the electromagnetic potential, V'(x) = V(x) + . The constant does not affect local dynamics in any way, but it does affect the cosmology. Since adding this constant adds a constant energy density to the universe, the continuity equation tells us that this is equivalent to a fluid with negative pressure, p = -. Einstein chose to give a closed, static universe as follows [2]. Take the energy density to consist of matter

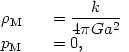(19)

and cosmological constant

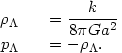(20)

It is a simple matter to use the Friedmann equation to show that this combination of matter and cosmological constant leads to a static universe = = 0. In order for the energy densities to be positive, the universe must be closed, k = + 1. Einstein was able to add a kludge to get the answer he wanted.

Things sometimes happen in science with uncanny timing. In the 1920's, an astronomer named Edwin Hubble undertook a project to measure the distances to the spiral "nebulae" as they had been known, using the 100-inch Mount Wilson telescope. Hubble's method involved using Cepheid variables, named after the star Delta Cephei, the best known member of the class. ⁽¹⁾ Cepheid variables have the useful property that the period of their variation, usually 10-100 days, is correlated to their absolute brightness. Therefore, by measuring the apparent brightness and the period of a distant Cepheid, one can determine its absolute brightness and therefore its distance. Hubble applied this method to a number of nearby galaxies, and determined that almost all of them were receding from the earth. Moreover, the more distant the galaxy was, the faster it was receding, according to a roughly linear relation:

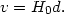(21)

This is the famous Hubble Law, and the constant H₀ is known as Hubble's constant. Hubble's original value for the constant was something like 500 km/sec/Mpc, where one megaparsec (Mpc) is a bit over 3 million light years. ⁽²⁾ This implied an age for the universe of about a billion years, and contradicted known geological estimates for the age of the earth. Cosmology had its first "age problem": the universe can't be younger than the things in it! Later it was realized that Hubble had failed to account for two distinct types of Cepheids, and once this discrepancy was taken into account, the Hubble constant fell to well under 100 km/s/Mpc. The current best estimate, determined using the Hubble space telescope to resolve Cepheids in galaxies at unprecedented distances, is H₀ = 71 ± 6 km/s/Mpc [5]. In any case, the Hubble law is exactly what one would expect from the Friedmann equation. The expansion of the universe predicted (and rejected) by Einstein had been observationally detected, only a few years after the development of General Relativity. Einstein later referred to the introduction of the cosmological constant as his "greatest blunder".

The expansion of the universe leads to a number of interesting things. One is the cosmological redshift of photons. The usual way to see this is that from the Hubble law, distant objects appear to be receding at a velocity v = H₀d, which means that photons emitted from the body are redshifted due to the recession velocity of the source. There is another way to look at the same effect: because of the expansion of space, the wavelength of a photon increases with the scale factor:

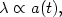(22)

so that as the universe expands, a photon propagating in the space gets shifted to longer and longer wavelengths. The redshift z of a photon is then given by the ratio of the scale factor today to the scale factor when the photon was emitted:

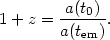(23)

Here we have introduced commonly used the convention that a subscript 0 (e.g., t₀ or H₀) indicates the value of a quantity today. This redshifting due to expansion applies to particles other than photons as well. For some massive body moving relative to the expansion with some momentum p, the momentum also "redshifts":

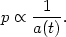(24)

We then have the remarkable result that freely moving bodies in an expanding universe eventually come to rest relative to the expanding coordinate system, the so-called comoving frame. The expansion of the universe creates a kind of dynamical friction for everything moving in it. For this reason, it will often be convenient to define comoving variables, which have the effect of expansion factored out. For example, the physical distance between two points in the expanding space is proportional to a(t). We define the comoving distance between two points to be a constant in time:

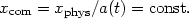(25)

Similarly, we define the comoving wavelength of a photon as

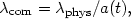(26)

and comoving momenta are defined as:

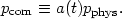(27)

This energy loss with expansion has a predictable effect on systems in thermal equilibrium. If we take some bunch of particles (say, photons with a black-body distribution) in thermal equilibrium with temperature T, the momenta of all these particles will decrease linearly with expansion, and the system will cool. ⁽³⁾ For a gas in thermal equilibrium, the temperature is in fact inversely proportional to the scale factor:

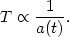(28)

The current temperature of the universe is about 3 K. Since it has been cooling with expansion, we reach the conclusion that the early universe must have been at a much higher temperature. This is the "Hot Big Bang" picture: a hot, thermal equilibrium universe expanding and cooling with time. One thing to note is that, although the universe goes to infinite density and infinite temperature at the Big Bang singularity, it does not necessarily go to zero size. A flat universe, for example is infinite in spatial extent an infinitesimal amount of time after the Big Bang, which happens everywhere in the infinite space simultaneously! The observable universe, as measured by the horizon size, goes to zero size at t = 0, but the observable universe represents only a tiny patch of the total space.

¹ Delta Cephei is not, however the nearest Cepheid. That honor goes to Polaris, the north star [3]. Back.

² The parsec is an archaic astronomical unit corresponding to one second of arc of parallax measured from opposite sides of the earth's orbit: 1 pc = 3.26 ly. Back.

³ It is not hard to convince yourself that a system that starts out as a blackbody stays a blackbody with expansion. Back.