Cosmology, Inflation, and the Physics of Nothing

2.4. The vacuum in quantum field theory

In this section, we will discuss something that at first glance appears to be entirely unrelated to cosmology: the vacuum in quantum field theory. We will see later, however, that it will in fact be crucially important to cosmology. Let us start with basic quantum mechanics, in the form of the simple harmonic oscillator, with Hamiltonian

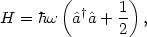(39)

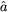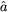where ahat and ahat ^† are the lowering and raising operators, respectively, with commutation relation

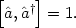(40)

This leads to the familiar ladder of energy eigenstates |n>,

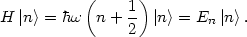(41)

The simple harmonic oscillator is pretty much the only problem that physicists know how to solve. Applying the old rule that if all you have is a hammer, everything looks like a nail, we construct a description of quantum fields by placing an infinite number of harmonic oscillators at every point,

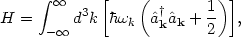(42)

where the operators ahat _k and ahat _k^† have the commutation relation

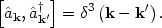(43)

Here we make the identification that k is the momentum of a particle, and omega _k is the energy of the particle,

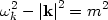(44)

for a particle of mass m. Taking m = 0 gives the familiar dispersion relation for massless particles like photons. Like the state kets |n> for the harmonic oscillator, each momentum vector k has an independent ladder of states, with the associated quantum numbers, |n_k ,..., n_k' >. The raising and lowering operators are now interpreted as creation and annihilation operators, turning a ket with n particles into a ket with n + 1 particles, and vice-versa:

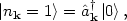(45)

and we call the ground state |0> the vacuum, or zero-particle state. But there is one small problem: just like the ground state of a single harmonic oscillator has a nonzero energy E₀ = (1/2) hbar omega , the vacuum state of the quantum field also has an energy,

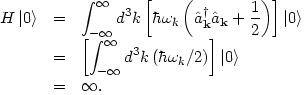(46)

The ground state energy diverges! The solution to this apparent paradox is that we expect quantum field theory to break down at very high energy. We therefore introduce a cutoff on the momentum k at high energy, so that the integral in Eq. (46) becomes finite. A reasonable physical scale for the cutoff is the scale at which we expect quantum gravitational effects to become relevant, the Planck scale m_Pl:

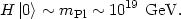(47)

Therefore we expect the vacuum everywhere to have a constant energy density, given in units where hbar = c = 1 as

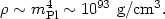(48)

But we have already met up with an energy density that is constant everywhere in space: Einstein's cosmological constant, rho = const., p = - rho . However, the cosmological constant we expect from quantum field theory is more than a hundred twenty orders of magnitude too big. In order for rho to be less than the critical density, Omega < 1, we must have rho < 10^-120m_Pl⁴! How can we explain this discrepancy? Nobody knows.