2.3. Critical density and the return of the age problem

One of the things that cosmologists most want to measure accurately is the total density of the universe. This is most often expressed in units of the density needed to make the universe flat, or k = 0. Taking the Friedmann equation for a k = 0 universe,

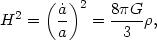(29)

we can define a critical density _c,

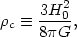(30)

which tells us, for a given value of the Hubble constant H₀, the energy density of a Euclidean FRW space. If the energy density is greater than critical, > _c, the universe is closed and has a positive curvature (k = + 1). In this case, the universe also has a finite lifetime, eventually collapsing back on itself in a "big crunch". If < _c, the universe is open, with negative curvature, and has an infinite lifetime. This is usually expressed in terms of the density parameter ,

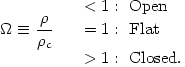(31)

There has long been a debate between theorists and observers as to what the value of is in the real universe. Theorists have steadfastly maintained that the only sensible value for is unity, = 1. This prejudice was further strengthened by the development of the theory of inflation, which solves several cosmological puzzles (see Secs. 4.1 and 4.2) and in fact predicts that will be exponentially close to unity. Observers, however, have made attempts to measure using a variety of methods, including measuring galactic rotation curves, the velocities of galaxies orbiting in clusters, X-ray measurements of galaxy clusters, the velocities and spatial distribution of galaxies on large scales, and gravitational lensing. These measurements have repeatedly pointed to a value of inconsistent with a flat cosmology, with = 0.2 - 0.3 being a much better fit, indicating an open, negatively curved universe. Until a few years ago, theorists have resorted to cheerfully ignoring the data, taking it almost on faith that = 0.7 in extra stuff would turn up sooner or later. The theorists were right: new observations of the cosmic microwave background definitively favor a flat universe, = 1. Unsurprisingly, the observationalists were also right: only about 1/3 of this density appears to be in the form of ordinary matter.

The first hint that something strange was up with the standard cosmology came from measurements of the colors of stars in globular clusters. Globular clusters are small, dense groups of 10⁵ - 10⁶ stars which orbit in the halos of most galaxies and are among the oldest objects in the universe. Their ages are determined by observation of stellar populations and models of stellar evolution, and some globular clusters are known to be at least 12 billion years old [4], implying that the universe itself must be at least 12 billion years old. But consider a flat universe ( = 1) filled with pressureless matter, a^-3 and p = 0. It is straightforward to solve the Friedmann equation (12) with k = 0 to show that

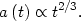(32)

The Hubble parameter is then given by

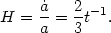(33)

We therefore have a simple expression for the age of the universe t₀ in terms of the measured Hubble constant H₀,

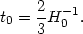(34)

The fact that the universe has a finite age introduces the concept of a horizon: this is just how far out in space we are capable of seeing at any given time. This distance is finite because photons have only traveled a finite distance since the beginning of the universe. Just as in special relativity, photons travel on paths with proper length ds² = dt² - a²dx² = 0, so that we can write the physical distance a photon has traveled since the Big Bang, or the horizon size, as

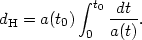(35)

(This is in units where the speed of light is set to c = 1.) For example, in a flat, matter-dominated universe, a(t) t^2/3, so that the horizon size is

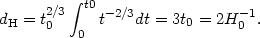(36)

This form for the horizon distance is true in general: the distance a photon travels in time t is always about d ~ t: effects from expansion simply add a numerical factor out front. We will frequently ignore this, and approximate

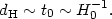(37)

Measured values of H₀ are quoted in a very strange unit of time, a km/s/Mpc, but it is a simple matter to calculate the dimensionless factor using 1 Mpc 3 × 10¹⁹ km, so that the age of a flat, matter-dominated universe with H₀ = 71 ± 6 km/s/Mpc is

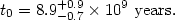(38)

A flat, matter-dominated universe would be younger than the things in it! Something is evidently wrong - either the estimates of globular cluster ages are too big, the measurement of the Hubble constant from from the HST is incorrect, the universe is not flat, or the universe is not matter dominated.

We will take for granted that the measurement of the Hubble constant is correct, and that the models of stellar structure are good enough to produce a reliable estimate of globular cluster ages (as they appear to be), and focus on the last two possibilities. An open universe, ₀ < 1, might solve the age problem. Figure 1 shows the age of the universe consistent with the HST Key Project value for H₀ as a function of the density parameter ₀.

Figure 1. Age of the universe as a function of 0 for a matter-dominated universe. The blue lines show the age t0 consistent with the HST key project value H0 = 72 ± 6 km/s/Mpc. The red area is the region consistent with globular cluster ages t0 > 12 Gyr.

We see that the age determined from H₀ is consistent with globular clusters as old as 12 billion years only for values of ₀ less than 0.3 or so. However, as we will see in Sec. 3, recent measurements of the cosmic microwave background strongly indicate that we indeed live in a flat ( = 1) universe. So while a low-density universe might provide a marginal solution to the age problem, it would conflict with the CMB. We therefore, perhaps reluctantly, are forced to consider that the universe might not be matter dominated. In the next section we will take a detour into quantum field theory seemingly unrelated to these cosmological issues. By the time we are finished, however, we will have in hand a different, and provocative, solution to the age problem consistent with a flat universe.