3.3. Acoustic oscillations and the horizon at last scattering
For fluctuation modes smaller than the horizon size, more complicated
physics comes into
play. Even a summary of the many effects that determine the precise
shape of the CMB
multipole spectrum is beyond the scope of these lectures, and the
student is referred
to Refs. [13]
for a more detailed discussion. However, the dominant process
that occurs on short wavelengths is important to us. These are
acoustic oscillations
in the baryon/photon plasma. The idea is simple: matter tends to
collapse due to gravity
onto regions where the density is higher than average, so the baryons
"fall" into overdense
regions. However, since the baryons and the photons are still strongly
coupled, the photons
tend to resist this collapse and push the baryons outward. The result is
"ringing", or
oscillatory modes of compression and rarefaction in the gas due to
density fluctuations. The
gas heats as it compresses and cools as it expands, and this creates
fluctuations in the
temperature of the CMB. This manifests itself in the
C
spectrum
as a series of
bumps (Fig. 8). The specific shape and location
of the bumps is created
by complicated, although well-understood physics, involving a large
number of cosmological
parameters. The shape of the CMB multipole spectrum depends, for
example, on the baryon density
b, the
Hubble constant H0, the densities of matter
M and
cosmological constant
,
and the amplitude of primordial gravitational waves (see
Sec. 4.5). This
makes interpretation of the spectrum something of a complex undertaking,
but it also makes it a sensitive probe of cosmological models. In these
lectures, I will primarily focus on the CMB as a probe of inflation, but
there is much more to the story.
These oscillations are sound waves in the direct sense: compression
waves in the gas. The position of the bumps in
is determined by the
oscillation frequency of the mode.
The first bump is created by modes that have had time to go through half
an oscillation in
the age of the universe (compression), the second bump modes that have
gone through
one full oscillation (rarefaction), and so on. So what is the wavelength
of a mode that
goes through half an oscillation in a Hubble time? About the horizon
size at the time
of recombination, 300,000 light years or so! This is an immensely
powerful tool: it
in essence provides us with a ruler of known length (the wavelength of
the oscillation
mode, or the horizon size at recombination), situated at a known
distance (the distance
to the surface of last scattering at z = 1100). The angular size
of this ruler when
viewed at a fixed distance depends on the curvature of the space that
lies between us
and the surface of last scattering (Fig. 7).
 |
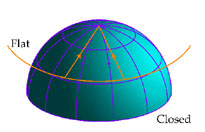Figure 7. The effect of geometry on angular size. Objects of a given angular size are smaller in a closed space than in a flat space. Conversely, objects of a given angular size are larger in an open space. (Figure courtesy of Wayne Hu [21].) |
If the space is negatively curved, the ruler will
subtend a smaller angle than if the space is flat;
(5)
if the space is positively curved, the
ruler will subtend a larger angle. We can measure the "angular size" of
our "ruler"
by looking at where the first acoustic peak shows up on the plot of the
C spectrum
of CMB fluctuations. The positions of the peaks are determined by the
curvature of the universe. (6)
This is how we measure
with the
CMB. Fig. 8 shows an
= 1 model and an
= 0.3 model
along with the current data. The data allow us to clearly distinguish
between flat and
open universes. Figure 9 shows limits from Type
Ia supernovae and the CMB in the space of
M and
.
 |
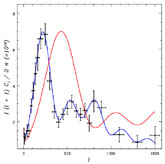Figure 8.
C |
 |
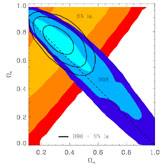Figure 9. Limits on
|
5 To paraphrase Gertrude Stein, "there's more there there." Back.
6 Not surprisingly, the real situation is a good deal more complicated than what I have described here. [13] Back.