4.5. Density fluctuations from inflation

So far we have seen that the standard FRW cosmology has two (related) unexplained issues: why is the universe so flat and why is it so smooth? These questions are difficult to answer in the context of a matter- or radiation-dominated cosmology without resorting to simply setting the initial conditions of the universe to match what we see, certainly an unsatisfying solution. The idea of inflation, a period of accelerated expansion in the very early universe, provides an elegant solution to these problems. At some early time, the energy density of the universe was dominated by something with an equation of state approximating that of vacuum energy, p < - (1/3). (In the discussion above, we considered a single scalar field as a model for such a fluid.) The useful thing about inflation is that it dynamically drives the universe toward a flat ( = 1) geometry, and simultaneously drives causally connected points to non-causal regions, explaining the homogeneity of the universe on scales larger than the horizon. This is an appealing scenario, but it is short on observational consequences: how do we tell whether or not inflation actually happened?

Very soon after the introduction of inflation by Guth, it was realized that inflation had another remarkable property: it could explain the generation of the primordial density fluctuations in the universe. This was first worked out independently by Hawking [29], Starobinsky [30], and by Guth [31]. We will cover the generation of fluctuations in great detail later, but the basic physics is familiar, and is closely related to the generation of Hawking radiation by black holes. It can be explained qualitatively as follows (Fig. 13). In a normal Minkowski space, vacuum fluctuations are interpreted as pairs of virtual particles appearing and then immediately annihilating as a consequence of the Heisenberg uncertainty principle. One qualitative explanation of Hawking radiation at the event horizon of a black hole is that one of the two virtual particles is trapped by the horizon, leaving the other to escape as apparently thermal radiation. A similar process holds in an inflationary spacetime: in inflation, the expansion is so rapid that pairs of virtual particles get "swept up" in the spacetime and are inflated to causally disconnected regions. In essence, they can no longer find each other to annihilate, and the quantum fluctuations become classical modes of the field.

Figure 13. Diagrams of virtual particles in a Minkowski space, near the horizon of a black hole, and in an inflationary space. Like the radiation created by one of the virtual pair being lost behind the horizon, virtual particles in inflation are swept out of each others' horizon before they can recombine.

Formally, this effect is calculated by considering the equation of motion for a fluctuation in a free field ,

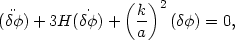(92)

where k is a comoving wavenumber which stays constant with expansion. The physical momentum p of the particle is

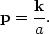(93)

During inflation, the wavelength of a quantum mode is "stretched" by the rapid expansion,

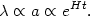(94)

The horizon size, however, remains roughly constant,

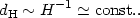(95)

Short-wavelength vacuum fluctuations are then quickly redshifted by the expansion until their wavelengths are larger than the horizon size of the spacetime, and the modes are "frozen" as classical fluctuations. The amplitudes of quantum modes in inflation are conventionally expressed at horizon crossing, that is when the wavelength of the mode is equal to the horizon size, or k/a = H. The two-point correlation function of the field at horizon crossing is just given by the Hubble parameter:

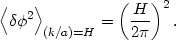(96)

Like the horizon of a black hole, the horizon of an inflationary space has a "temperature" T ~ H^-1. The simplest example of the creation of fluctuations during inflation is the generation of gravitational waves, or tensor modes. An arbitrary perturbation to the metric tensor can be expressed as a sum scalar, vector, and tensor fluctuations, depending on how each behaves under coordinate transformations,

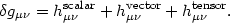(97)

The tensor component can be expressed in general as the superposition of two gravitational wave modes,

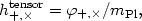(98)

where + , × refer to longitudinal and transverse polarization modes, respectively. Each mode has the equation of motion of a free scalar during inflation. Therefore fluctuations in the field are generated by the rapid expansion,

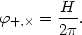(99)

The case of scalar fluctuations is more complex, since scalar modes are generated by fluctuations in the inflaton field itself and couple to the curvature of the spacetime. We will simply note the correct expression, ⁽⁹⁾

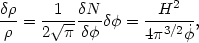(100)

where N is the number of e-folds of inflation,

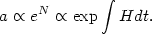(101)

What about vector modes, or primordial vorticity? Since there is no way to source such modes with a single scalar field, primordial vector perturbations vanish, at least in simple models of inflation.

⁹ The convention for normalizing this expression varies in the literature. Back.