Cosmology, Inflation, and the Physics of Nothing

4.2. The horizon problem

There is another odd fact about the observed universe: the apparent high degree of uniformity and thermal equilibrium of the CMB. While it might at first seem quite natural for the hot gas of the early universe to be in good thermal equilibrium, this is in fact quite unnatural in the standard Big Bang picture. This is because of the presence of a cosmological horizon. We recall that the horizon size of the universe is just how far a photon can have traveled since the Big Bang, d_H ~ t in units where c = 1. This defines how large a "patch" of the universe can be in causal contact. Two points in the universe separated by more than a horizon size have no way to reach thermal equilibrium, since they cannot have ever been in causal contact. Consider two points comoving with respect to the cosmological expansion. The physical distance d between the two points then just increases linearly with the scale factor:

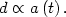(63)

The horizon size is just proportional to the time, or equivalently to the inverse of the Hubble parameter,

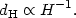(64)

It is straightforward to show that for any FRW space with constant equation of state, there is a conserved quantity given by

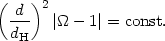(65)

Proof of this is also left as an exercise for the student. If we again consider the case of "ordinary" matter, with equation of state 1 + 3w > 0, we see from Eqs. (61) and (65) that the horizon expands faster than a comoving length:

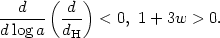(66)

This means that any two points at rest relative to the expansion of the universe will be causally disconnected at early times and causally connected at late times. This can be visualized on a conformal space-time diagram (Fig. 10). On a conformal diagram, we re-write the metric in terms of conformal time d tau ident dt/a:

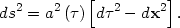(67)

The advantage of this choice of coordinates is that light always travels at 45° angles dx = d tau on the diagram, regardless of the behavior of the scale factor. In a matter dominated universe, the scale factor evolves as

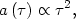(68)

so the Big Bang, a = 0, is a surface x = const. at tau = 0. Two points on a given tau = const. surface are in causal contact if their past light cones intersect at the Big Bang, tau = 0.

Figure 10. Light cones in a FRW space, plotted in conformal coordinates, ds² = a²(d tau ² - dx²). The "Big Bang" is a surface at tau = 0. Points in the space can only be in causal contact if their past light cones intersect at the Big Bang.

So the natural expectation for the very early universe is that there should be a large number of small, causally disconnected regions that will be in poor thermal equilibrium. The central question is: just how large was the horizon when the CMB was emitted? Since the universe was about 300,000 years old at recombination, the horizon size then was about 300,000 light years. Each atom at the surface of last scattering could only be in causal contact (and therefore in thermal equilibrium) with with other atoms within a radius of about 300,000 light years. As seen from earth, the horizon size at the surface of last scattering subtends an angle on the sky of about a degree.

Figure 11. Schematic diagram of the horizon size at the surface of last scattering. The horizon size at the time of recombination was about 300,000 light years. Viewed from earth, this subtends an angle of about a degree on the sky.

Therefore, two points on the surface of last scattering separated by an angle of more than a degree were out of causal contact at the time the CMB was emitted. However, the CMB is uniform (and therefore in thermal equilibrium) over the entire sky to one part in 10⁵. How did all of these disconnected regions reach such a high degree of thermal equilibrium?