


4.3. Inflation
The flatness and horizon problems have no solutions within the context of a standard matter- or radiation-dominated universe, since for any ordinary matter, the force of gravity causes the expansion of the universe to decelerate. The only available fix would appear to be to invoke initial conditions: the universe simply started out flat, hot, and in thermal equilibrium. While this is certainly a possibility, it hardly a satisfying explanation. It would be preferable to have an explanation for why the universe was flat, hot, and in thermal equilibrium. Such an explanation was proposed by Alan Guth in 1980 [25] under the name of inflation. Inflation is the idea that at some very early epoch, the expansion of the universe was accelerating instead of decelerating.
Accelerating expansion turns the horizon and flatness problems on their heads. This is evident from the equation for the acceleration,
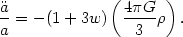 |
(69) |
We see immediately that the condition for acceleration
 > 0 is that the
equation of state be characterized by negative pressure,
1 + 3w < 0. This
means that the universe evolves toward flatness rather than away:
> 0 is that the
equation of state be characterized by negative pressure,
1 + 3w < 0. This
means that the universe evolves toward flatness rather than away:
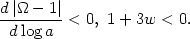 |
(70) |
Similarly, from Eq. (65), we see that comoving scales grow in size more quickly than the horizon,
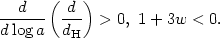 |
(71) |
This is a very remarkable behavior. It means that two points that are initially in causal contact (d < dH) will expand so rapidly that they will eventually be causally disconnected. Put another way, two points in space whose relative velocity due to expansion is less than the speed of light will eventually be flying apart from each other at greater than the speed of light! Note that there is absolutely no violation of the principles of relativity. Relative velocities v > c are allowed in general relativity as long as the observers are sufficiently separated in space. (7) This mechanism provides a neat way to explain the apparent homogeneity of the universe on scales much larger than the horizon size: a tiny region of the universe, initially in some sort of equilibrium, is "blown up" by accelerated expansion to an enormous and causally disconnected scale.
We can plot the inflationary universe on a conformal diagram (Fig. 12).
In an inflationary universe, there is no singularity
a  0 at
conformal time
0 at
conformal time
 = 0. To see this, take the
case of a cosmological constant,
= 0. To see this, take the
case of a cosmological constant,

 =
const., which corresponds to exponential increase of the scale factor:
=
const., which corresponds to exponential increase of the scale factor:
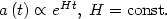 |
(72) |
In this case, the conformal time is negative and evolves toward zero with increasing "proper" time t:
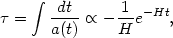 |
(73) |
so that the scale factor evolves as
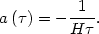 |
(74) |
The scale factor becomes infinite at
 = 0! This is because we
have assumed H = const.,
which means that inflation will continue forever, with
= 0! This is because we
have assumed H = const.,
which means that inflation will continue forever, with
 = 0 representing the
infinite future,
t
= 0 representing the
infinite future,
t 
 . In the real universe,
inflation ends at some finite time, and the
approximation (74), while valid at early times, breaks down near the end
of inflation.
So the surface
. In the real universe,
inflation ends at some finite time, and the
approximation (74), while valid at early times, breaks down near the end
of inflation.
So the surface  = 0 is not
the Big Bang, but the end of inflation. The initial singularity
has been pushed back arbitrarily far in conformal time
= 0 is not
the Big Bang, but the end of inflation. The initial singularity
has been pushed back arbitrarily far in conformal time
 << 0, and light cones
can extend through the apparent "Big Bang" so that apparently
disconnected points are in causal contact.
<< 0, and light cones
can extend through the apparent "Big Bang" so that apparently
disconnected points are in causal contact.
How much inflation do we need to solve the horizon and flatness problems? We will see that sensible models of inflation tend to place the inflationary epoch at a time when the temperature of the universe was typical of Grand Unification,
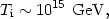 |
(75) |
so that the horizon size, or size of a causal region, was about
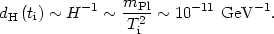 |
(76) |
In order for inflation to solve the horizon problem, this causal region must be blown up to at least the size of the observable universe today, (8)
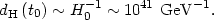 |
(77) |
So that the scale factor must increase by about
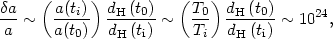 |
(78) |
or somewhere around a factor of e55. Here the extra factor a(ti) / a(t0) accounts for the expansion between the end of inflation Ti ~ 1015 GeV and today, T0 ~ 10-4 eV. This is the minimum amount of inflation required to solve the horizon problem, and inflation can in fact go on for much longer. In the next section we will talk about how one constructs a model of inflation in particle theory. A more detailed introductory review can be found in Ref. [26].
7 An interesting consequence of the currently observed accelerating expansion is that all galaxies except those in our local group will eventually be moving away from us faster than the speed of light and will be invisible to us. The far future universe will be a lonely place, and cosmology will be all but impossible! Back.
8 Exercise for the student: what is 1 km/s/MpC measured in units of GeV? Back.