4.4. Inflation from scalar fields

We have already seen that a cosmological constant due to nonzero vacuum energy results in accelerating cosmological expansion. While this is a good candidate for explaining the observations of Type Ia supernovae, it does not work for explaining inflation at early times for the simple reason that any period of accelerated expansion in the very early universe must end. Therefore the vacuum energy driving inflation must be dynamic. To implement a time-dependent "cosmological constant," we require a field with the same quantum numbers as vacuum, i.e. a scalar. We will consider a scalar field minimally coupled to gravity, with potential V() and Lagrangian

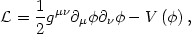(79)

where we have modified a familiar Minkowski-space field theory by replacing the Minkowski metric ^µ with the FRW metric g^µ. The equation of motion for the field is

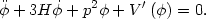(80)

This is the familiar equation for a free scalar field with an extra piece, 3H, that comes from the use of the FRW metric in the Lagrangian. We will be interested in the ground state of the field p = 0. This is of interest because the zero mode of the field forms a perfect fluid, with energy density

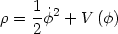(81)

and pressure

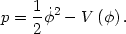(82)

Note in particular that in the limit 0 we recover a cosmological constant, p = - , as long as the potential V() is nonzero. The Friedmann equation for the dynamics of the cosmology is

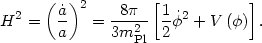(83)

(Note that we have written Newtons' constant G in terms of the Planck mass, so that G = m_Pl^-2 in units where = c = 1.) In the 0 limit, we have

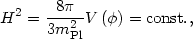(84)

so that the universe expands exponentially,

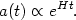(85)

This can be generalized to a time-dependent field and a quasi-exponential expansion in a straightforward way. If we have a slowly varying field (1/2)² << V(), we can write the equation of motion of the field as

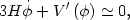(86)

and the Friedmann equation as

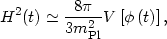(87)

so that the scale factor evolves as

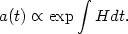(88)

This is known as the slow roll approximation, and corresponds physically to the field evolution being dominated by the "friction" term 3H in the equation of motion. This will be the case if the potential is sufficiently flat, V'() << V(). It is possible to write the equation of state of the field in the slow roll approximation as

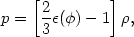(89)

where the slow roll parameter is given by

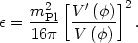(90)

This parameterization is convenient because the condition for accelerating expansion is < 1:

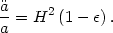(91)

Specifying a model for inflation is then as simple as selecting a potential V() and evaluating its behavior as a source of cosmological energy density. Many models have been proposed: Refs. [27, 28] contain extensive reviews of inflationary model building. We will discuss the observational predictions of various models in Section 4.8 below. In the next section, we will discuss one of the central observational predictions of inflation: the generation of primordial density fluctuations.