10.2. Temperature of horizons

There exists a natural definition of QFT in the original (D + 1)-dimensional space; in particular, we can define a vacuum state for the quantum field on the Z⁰ = 0 surface, which coincides with the t = 0 surface. By restricting the field modes (or the field configurations in the Schrodinger picture) to depend only on the coordinates in , we will obtain a quantum field theory in in the sense that these modes will satisfy the relevant field equation defined in . In general, this is a complicated problem and it is not easy to have a choice of modes in which will lead to a natural set of modes in . We can, however, take advantage of the arguments given in the last section - that all the interesting physics arises from the (Z⁰, Z¹) plane and the other transverse dimensions are irrelevant near the horizon. In particular, solutions to the wave equation in which depends only on the coordinates Z⁰ and Z¹ will satisfy the wave equation in and will depend only on (t, r). Such modes will define a natural s-wave QFT in . The positive frequency modes of the above kind (varying as exp(- i Z⁰) with > 0.) will be a specific superposition of negative (varying as e^{i t}) and positive (varying as e^{-i t}) frequency modes in leading to a temperature T = (g / 2) in the 4-dimensional subspace on one side of the horizon. There are several ways of proving this result, all of which depend essentially on the property that under the transformation t t ± (i / g) the two coordinates Z⁰ and Z¹ reverses sign.

Consider a positive frequency mode of the form F(Z⁰, Z¹) exp[- i Z⁰ + iPZ¹] with > 0. These set of modes can be used to expand the quantum field thereby defining the creation and annihilation operators A, A^†:

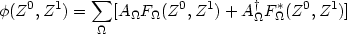(166)

The vacuum state defined by A| vac > = 0 corresponds to a globally time symmetric state which will be interpreted as a no particle state by observers using Z⁰ as the time coordinate. Let us now consider the same mode which can be described in terms of the (t, r) coordinates. Being a scalar, this mode can be expressed in the 4-dimensional sector in the form F(t, r) = F [Z⁰(t, r), Z¹(t, r)]. The Fourier transform of F(t, r) with respect to t will be:

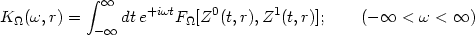(167)

Thus a positive frequency mode in the higher dimension can only be expressed as an integral over with ranging over both positive and negative values. However, using the fact that t t - (i / g) leads to Z⁰ - Z¹, it is easy to show that

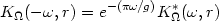(168)

This allows us to write the inverse relation to (167) as

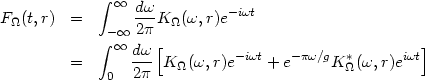(169)

The term with K^* represents the contribution of negative frequency modes in the the 4-D spacetime to the pure positive frequency mode in the embedding spacetime. A field mode of the embedding spacetime containing creation and annihilation operators (A, A^†) can now be represented in terms of the creation and annihilation operators (a, a^†) appropriate to the (t, r) coordinates as

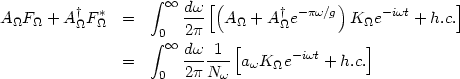(170)

where N is a normalization constant. Identifying a = N(A + e^{- / g} A^†) and using the conditions [a, a^†] = 1, [A, A^†] = 1 etc., we get N = [1 - exp(- 2 / g)]^-1/2. It follows that the number of a -particles in the vacuum defined by A| vac > = 0 is given by

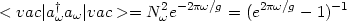(171)

This is a Planckian spectrum with temperature T = g / 2. The key role in the derivation is played by equation (168) which, in turn, arises from the analytic properties of the spacetime under Euclidean continuation.