


10.3. Entropy and energy of de Sitter spacetime
The best studied spacetimes with horizons are the black hole
spacetimes. (For a sample of references, see
[297,
298,
299,
300,
301,
302,
303,
304,
305,
306]).
In the simplest context of a Schwarzschild black hole of mass M,
one can attribute an energy E = M, temperature
T = (8 M)-1 and entropy
S = (1/4)(AH /
LP2) where AH is the area
of the horizon and
LP = (G
M)-1 and entropy
S = (1/4)(AH /
LP2) where AH is the area
of the horizon and
LP = (G
 /
c3)1/2 is the Planck length. (Hereafter, we
will use units with
G =
/
c3)1/2 is the Planck length. (Hereafter, we
will use units with
G =  = c =
1.) These are clearly related by the thermodynamic identity
TdS = dE, usually called the first law of black hole
dynamics. This result has been obtained in much more general contexts
and has been investigated from many different points of view in the
literature. The simplicity of the result depends on the following
features: (a) The Schwarzschild metric is a vacuum solution
with no pressure so that there is no PdV term in the first law of
thermodynamics. (b) The metric has only one parameter M so that
changes in all physical parameters can be related to dM. (c) Most
importantly, there exists a well defined notion of energy E to
the spacetime and the changes in the energy dE can be interpreted
in terms of the physical process of the black hole evaporation. The idea
can be generalized to other black hole spacetimes in a rather simple
manner only because of well defined notions of energy, angular momentum etc.
= c =
1.) These are clearly related by the thermodynamic identity
TdS = dE, usually called the first law of black hole
dynamics. This result has been obtained in much more general contexts
and has been investigated from many different points of view in the
literature. The simplicity of the result depends on the following
features: (a) The Schwarzschild metric is a vacuum solution
with no pressure so that there is no PdV term in the first law of
thermodynamics. (b) The metric has only one parameter M so that
changes in all physical parameters can be related to dM. (c) Most
importantly, there exists a well defined notion of energy E to
the spacetime and the changes in the energy dE can be interpreted
in terms of the physical process of the black hole evaporation. The idea
can be generalized to other black hole spacetimes in a rather simple
manner only because of well defined notions of energy, angular momentum etc.
Can one generalize the thermodynamics of horizons to cases other than black holes in a straight forward way ? In spite of years of research in this field, this generalization remains non trivial and challenging when the conditions listed above are not satisfied. To see the importance of the above conditions, we only need to contrast the situation in Schwarzschild spacetime with that of de Sitter spacetime:
 where H-1 is the radius of the de Sitter horizon. But
the correspondence probably ends there. A study of literature shows that
there exist very few concrete calculations of energy, entropy and laws
of horizon dynamics in the case of de Sitter spacetimes, in sharp
contrast to BH space times.
where H-1 is the radius of the de Sitter horizon. But
the correspondence probably ends there. A study of literature shows that
there exist very few concrete calculations of energy, entropy and laws
of horizon dynamics in the case of de Sitter spacetimes, in sharp
contrast to BH space times.
All these suggest that to make any progress, one might require a local approach by which one can define the notion of entropy and energy for spacetimes with horizons. This conclusion is strengthened further by the following argument: Consider a class of spherically symmetric spacetimes of the form
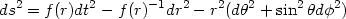 |
(172) |
If f (r) has a simple zero at r = a with
f'(a)  B remaining finite, then
this spacetime has a horizon at r = a.
Spacetimes like Schwarzschild or de Sitter have only one free parameter
in the metric (like M or H-1) and hence the
scaling of all other thermodynamical parameters is uniquely fixed by
purely dimensional considerations. But, for a general metric
of the form in (172), with an arbitrary f (r), the
area of the horizon (and hence the entropy) is determined by the
location of the zero of the function f (r) while the
temperature - obtained from the periodicity considerations -
is determined by the value of f'(r) at the zero. For a
general function, of course, there will be no relation between the
location of the zero and the slope of the function at that point. It
will, therefore, be incredible if there exists any a priori relationship
between the temperature (determined by f' ) and the entropy
(determined by the zero of f) even in the context of horizons in
spherically symmetric spacetimes. If we take the entropy to be S
=
B remaining finite, then
this spacetime has a horizon at r = a.
Spacetimes like Schwarzschild or de Sitter have only one free parameter
in the metric (like M or H-1) and hence the
scaling of all other thermodynamical parameters is uniquely fixed by
purely dimensional considerations. But, for a general metric
of the form in (172), with an arbitrary f (r), the
area of the horizon (and hence the entropy) is determined by the
location of the zero of the function f (r) while the
temperature - obtained from the periodicity considerations -
is determined by the value of f'(r) at the zero. For a
general function, of course, there will be no relation between the
location of the zero and the slope of the function at that point. It
will, therefore, be incredible if there exists any a priori relationship
between the temperature (determined by f' ) and the entropy
(determined by the zero of f) even in the context of horizons in
spherically symmetric spacetimes. If we take the entropy to be S
=  a2 (where
f (a) = 0 determines the radius of the horizon) and
the temperature to be T = | f'(a)| /
4
a2 (where
f (a) = 0 determines the radius of the horizon) and
the temperature to be T = | f'(a)| /
4 (determined by the
periodicity of Euclidean time), the quantity
TdS = (1/2)| f'(a)| a da will depend both on
the slope f'(a) as well as
the radius of the horizon. This implies that any local interpretation of
thermodynamics will be quite non trivial.
(determined by the
periodicity of Euclidean time), the quantity
TdS = (1/2)| f'(a)| a da will depend both on
the slope f'(a) as well as
the radius of the horizon. This implies that any local interpretation of
thermodynamics will be quite non trivial.
Finally, the need for local description of thermodynamics of horizons becomes crucial in the case of spacetimes with multiple horizons. The strongest and the most robust result we have, regarding spacetimes with a horizon, is the notion of temperature associated with them. This, in turn, depends on the study of the periodicity of the Euclidean time coordinate. This approach does not work very well if the spacetime has more than one horizon like, for example, in the Schwarzschild-de Sitter metric which has the form in (172) with
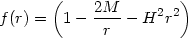 |
(173) |
This spacetime has two horizons at r ± with
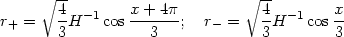 |
(174) |
where cos x = - 3 3
MH-1. (The parameter x is in the range
(
3
MH-1. (The parameter x is in the range
( ,
(3/2)
,
(3/2) ] and
we assume that 0
] and
we assume that 0  27M2H-2 < 1.)
Close to either horizon the spacetime can be approximated as Rindler.
Since the surface gravities on the two
horizons are different, we get two different temperatures
T ± = | f'(r ± )|
/ 4
27M2H-2 < 1.)
Close to either horizon the spacetime can be approximated as Rindler.
Since the surface gravities on the two
horizons are different, we get two different temperatures
T ± = | f'(r ± )|
/ 4 .
To maintain invariance under
it
.
To maintain invariance under
it  it +
it +  (with some finite
(with some finite
 ) it is necessary
that
) it is necessary
that  is an
integer multiple of both 4
is an
integer multiple of both 4 /
| f'(r+)| and
4
/
| f'(r+)| and
4 /
| f'(r-)| so that
/
| f'(r-)| so that
 =
(4
=
(4 n ±
/ | f'(r ± )|) where n ±
are integers. Hence the ratio of surface gravities
| f'(r+)| /
| f'(r-)| =
(n+/n-) must be a rational number.
Though irrationals can be approximated by rationals,
such a condition definitely excludes a class of values for
M if H is specified and vice versa.
It is not clear why the existence of a cosmological constant
should imply something for the masses of black holes (or vice versa).
Since there is no physical basis for such a condition,
it seems reasonable to conclude that these difficulties arise
because of our demanding the existence of a finite periodicity
n ±
/ | f'(r ± )|) where n ±
are integers. Hence the ratio of surface gravities
| f'(r+)| /
| f'(r-)| =
(n+/n-) must be a rational number.
Though irrationals can be approximated by rationals,
such a condition definitely excludes a class of values for
M if H is specified and vice versa.
It is not clear why the existence of a cosmological constant
should imply something for the masses of black holes (or vice versa).
Since there is no physical basis for such a condition,
it seems reasonable to conclude that these difficulties arise
because of our demanding the existence of a finite periodicity
 in the
Euclidean time coordinate. This demand is related to
an expectation of thermal equilibrium which is violated in spacetimes with
multiple horizons having different temperatures.
in the
Euclidean time coordinate. This demand is related to
an expectation of thermal equilibrium which is violated in spacetimes with
multiple horizons having different temperatures.
If even the simple notion of temperature falls apart in the presence of multiple horizons, it is not likely that the notion of energy or entropy can be defined by global considerations. On the other hand, it will be equally strange if we cannot attribute a temperature to a black hole formed in some region of the universe just because the universe at the largest scales is described by a de Sitter spacetime, say. One is again led to searching for a local description of the thermodynamics of all types of horizons. We shall now see how this can be done.
Given the notion of temperature, there are two very different ways of
defining the entropy: (1) In statistical mechanics, the partition
function
Z( )
of the canonical ensemble of systems with constant temperature
)
of the canonical ensemble of systems with constant temperature
 -1
is related to the entropy S and energy E by
Z(
-1
is related to the entropy S and energy E by
Z( )
)
 exp(S -
exp(S -
 E).
(2) In classical thermodynamics, on the other hand, it is the change
in the entropy, which can be operationally defined via
dS = dE / T(E). Integrating this equation will
lead to the function S(E) except for an additive constant
which needs to be determined from additional considerations. Proving the
equality of these two concepts was nontrivial and - historically - led
to the unification of thermodynamics with mechanics.
E).
(2) In classical thermodynamics, on the other hand, it is the change
in the entropy, which can be operationally defined via
dS = dE / T(E). Integrating this equation will
lead to the function S(E) except for an additive constant
which needs to be determined from additional considerations. Proving the
equality of these two concepts was nontrivial and - historically - led
to the unification of thermodynamics with mechanics.
In the case of time symmetric state, there will be no change of entropy
dS and the thermodynamic
route is blocked. It is, however, possible to construct a canonical
ensemble of a class of spacetimes and evaluate the partition function
Z( ).
For spherically symmetric spacetimes with a horizon at r =
l, the partition function has the generic form
Z
).
For spherically symmetric spacetimes with a horizon at r =
l, the partition function has the generic form
Z  exp[S -
exp[S -
 E],
where S = (1/4)4
E],
where S = (1/4)4 l2 and | E| = (l /2). This analysis
reproduces the conventional result for the black hole spacetimes and
provides a simple and consistent interpretation of entropy and energy
for de Sitter spacetime, with the latter being given by
E = - (1/2)H-1.
In fact, it is possible to write Einstein's equations for a spherically
symmetric spacetime as a thermodynamic identity
TdS - dE = PdV with T, S and E
determined as above and the PdV term arising from the
source [293].
We shall now discuss some of these issues.
l2 and | E| = (l /2). This analysis
reproduces the conventional result for the black hole spacetimes and
provides a simple and consistent interpretation of entropy and energy
for de Sitter spacetime, with the latter being given by
E = - (1/2)H-1.
In fact, it is possible to write Einstein's equations for a spherically
symmetric spacetime as a thermodynamic identity
TdS - dE = PdV with T, S and E
determined as above and the PdV term arising from the
source [293].
We shall now discuss some of these issues.
Consider a class of spacetimes with the metric
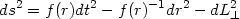 |
(175) |
where f (r) vanishes at some surface r = l,
say, with f'(l)
 B remaining
finite. When
dL
B remaining
finite. When
dL 2 = r2
dS22 with
[0
2 = r2
dS22 with
[0  r
r

 ], equation (175) covers
a variety of spherically symmetric spacetimes with a compact horizon at
r = l. Since the metric is static, Euclidean continuation
is trivially effected by
t
], equation (175) covers
a variety of spherically symmetric spacetimes with a compact horizon at
r = l. Since the metric is static, Euclidean continuation
is trivially effected by
t 
 = it and an
examination of the conical singularity near r = a [where
f (r)
= it and an
examination of the conical singularity near r = a [where
f (r)  B(r - a)] shows that
B(r - a)] shows that
 should be interpreted as
periodic with period
should be interpreted as
periodic with period
 =
4
=
4 /
| B| corresponding to the temperature
T = | B| / 4
/
| B| corresponding to the temperature
T = | B| / 4 .
Let us consider a set
.
Let us consider a set
 of such metrics in
(175) with the restriction that
[f (a) = 0, f'(a) = B] but f
(r) is otherwise arbitrary and has no
zeros. The partition function for this set of metrics
of such metrics in
(175) with the restriction that
[f (a) = 0, f'(a) = B] but f
(r) is otherwise arbitrary and has no
zeros. The partition function for this set of metrics
 is given by the path
integral sum
is given by the path
integral sum
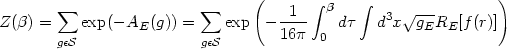 |
(176) |
where Einstein action has been continued in the Euclidean sector
and we have imposed the periodicity in
 with period
with period
 =
4
=
4 / | B|.
The sum is restricted to the set
/ | B|.
The sum is restricted to the set
 of all metrics of
the form in (175) with the behaviour
[f (a) = 0, f'(a) = B] and the
Euclidean Lagrangian is a functional of f (r).
The spatial integration will be restricted to a region bounded by the
2-spheres r = a and r = b, where
the choice of b is arbitrary except for the requirement that
within the region of integration the Lorentzian metric must have the
proper signature with t being a time coordinate. The remarkable
feature is the form of the Euclidean action for this class of
spacetimes. Using the result R =
of all metrics of
the form in (175) with the behaviour
[f (a) = 0, f'(a) = B] and the
Euclidean Lagrangian is a functional of f (r).
The spatial integration will be restricted to a region bounded by the
2-spheres r = a and r = b, where
the choice of b is arbitrary except for the requirement that
within the region of integration the Lorentzian metric must have the
proper signature with t being a time coordinate. The remarkable
feature is the form of the Euclidean action for this class of
spacetimes. Using the result R =
 r2
f - (2/r2)(d / dr)(r(1 -
f )) valid for metrics of the form in (175), a
straight forward calculation shows that
r2
f - (2/r2)(d / dr)(r(1 -
f )) valid for metrics of the form in (175), a
straight forward calculation shows that
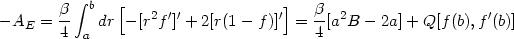 |
(177) |
where Q depends on the behaviour of the metric near r =
b and we have used the conditions
[f (a) = 0, f'(a) = B]. The sum in
(176) now reduces to summing over the values of
[f (b), f'(b)]
with a suitable (but unknown) measure.
This sum, however, will only lead to a factor which we can ignore in
deciding about the dependence of
Z( )
on the form of the metric near r = a. Using
)
on the form of the metric near r = a. Using
 =
4
=
4 / B
(and taking B > 0, for the moment) the final result can be
written in a very suggestive form:
/ B
(and taking B > 0, for the moment) the final result can be
written in a very suggestive form:
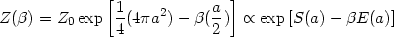 |
(178) |
with the identifications for the entropy and energy being given by:
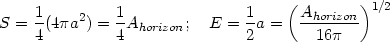 |
(179) |
In the case of the Schwarzschild black hole with a = 2M,
the energy turns out to be
E = (a/2) = M which is as expected. (More generally,
E = (Ahorizon /
16 )1/2 corresponds
to the so called `irreducible mass' in BH spacetimes
[316].)
Of course, the identifications
S = (4
)1/2 corresponds
to the so called `irreducible mass' in BH spacetimes
[316].)
Of course, the identifications
S = (4 M2), E = M,
T = (1/8
M2), E = M,
T = (1/8 M) are consistent with the result dE = TdS in this
particular case.
M) are consistent with the result dE = TdS in this
particular case.
The above analysis also provides an interpretation of entropy and energy
in the case of de Sitter universe. In this case,
f (r) = (1 - H2 r2),
a = H-1, B = - 2H.
Since the region where t is time like is "inside" the horizon,
the integral for AE in (177) should be taken from some
arbitrary value r = b to r = a with a
> b. So the horizon contributes in the upper limit of the
integral introducing a change of sign in (177). Further, since B
< 0, there is another negative sign in the area term from
 B
B
 B / |
B|. Taking all these into account we get, in this case,
B / |
B|. Taking all these into account we get, in this case,
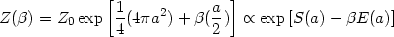 |
(180) |
giving S = (1/4)(4 a2) = (1/4)Ahorizon and
E = - (1/2)H-1.
These definitions do satisfy the relation
TdS - PdV = dE when it is noted that the de Sitter
universe has a non zero pressure
P = -
a2) = (1/4)Ahorizon and
E = - (1/2)H-1.
These definitions do satisfy the relation
TdS - PdV = dE when it is noted that the de Sitter
universe has a non zero pressure
P = - 
 = - E/V associated with the
cosmological constant. In fact,
if we use the "reasonable" assumptions
S = (1/4)(4
= - E/V associated with the
cosmological constant. In fact,
if we use the "reasonable" assumptions
S = (1/4)(4 H-2), V
H-2), V
 H-3 and E = - PV in the equation
TdS - PdV = dE and treat E as an unknown
function of H, we get the equation
H2(dE / dH) = - (3EH + 1)
which integrates to give precisely
E = - (1/2)H-1.
(Note that we only needed the proportionality,
V
H-3 and E = - PV in the equation
TdS - PdV = dE and treat E as an unknown
function of H, we get the equation
H2(dE / dH) = - (3EH + 1)
which integrates to give precisely
E = - (1/2)H-1.
(Note that we only needed the proportionality,
V  H-3 in this argument since
PdV
H-3 in this argument since
PdV  (dV/V). The ambiguity between the coordinate and proper
volume is irrelevant.)
(dV/V). The ambiguity between the coordinate and proper
volume is irrelevant.)
A peculiar feature of the metrics in (175) is worth stressing.
This metric will satisfy Einstein's equations provided the the source
stress tensor has the form
Ttt = Trr
 (
( (r) /
8
(r) /
8 );
T
);
T
 =
T
=
T

 (µ(r)
/ 8
(µ(r)
/ 8 ).
The Einstein's equations now reduce to:
).
The Einstein's equations now reduce to:
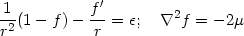 |
(181) |
The remarkable feature about the metric in (175) is that the Einstein's
equations become linear in f (r) so that solutions for
different  (r)
can be superposed. Given any
(r)
can be superposed. Given any
 (r) the
solution becomes
(r) the
solution becomes
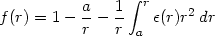 |
(182) |
with a being an integration constant and µ(r)
is fixed by
 (r) through:
µ(r) =
(r) through:
µ(r) =
 + (1/2)r
+ (1/2)r
 '(r).
The integration constant a in (182) is chosen such that f
(r) = 0 at r = a so that this surface
is a horizon. Let us now assume that the solution (182) is such that
f (r) = 0 at r = a with
f'(a) = B finite leading to leading to a notion of
temperature with
'(r).
The integration constant a in (182) is chosen such that f
(r) = 0 at r = a so that this surface
is a horizon. Let us now assume that the solution (182) is such that
f (r) = 0 at r = a with
f'(a) = B finite leading to leading to a notion of
temperature with
 =
(4
=
(4 / | B|).
From the first of the equations (181) evaluated at r = a,
we get
/ | B|).
From the first of the equations (181) evaluated at r = a,
we get
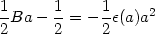 |
(183) |
It is possible to provide an interesting interpretation of this equation
which throws light on the notion of entropy and energy.
Multiplying the above equation by da and using
 =
8
=
8 Trr, it is trivial to rewrite equation (183)
in the form
Trr, it is trivial to rewrite equation (183)
in the form
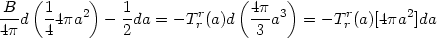 |
(184) |
Let us first consider the case in which a particular horizon has
f'(a) = B > 0 so that the temperature is
T = B / 4 .
Since
f (a) = 0, f'(a) > 0, it follows that
f > 0 for r > a and f < 0 for
r < a; that is, the "normal region" in which t
is time like is outside
the horizon as in the case of, for example, the Schwarzschild metric.
The first term in the left hand side of (184) clearly has the form of
TdS since we have an independent identification of temperature
from the periodicity argument in the local Rindler coordinates.
Since the pressure is P = - Trr,
the right hand side has the structure of PdV or - more
relevantly - is the product of the radial pressure times the transverse
area times the radial displacement. This is important because, for the
metrics in the form (175), the proper transverse area is just that of a
2-sphere though the proper volumes and coordinate volumes differ.
In the case of horizons with B = f'(a) > 0 which
we are considering (with da > 0), the volume of the region
where f < 0 will increase and the volume of the region
where f > 0 will decrease.
Since the entropy is due to the existence of an inaccessible region,
dV must refer to the change in the volume of the inaccessible
region where f < 0. We can now identify
T in TdS and P in PdV without any difficulty
and interpret the remaining term (second term in the left hand side) as
dE = da/2. We thus get the expressions for the entropy
S and energy E (when B > 0) to be
the same as in (179).
.
Since
f (a) = 0, f'(a) > 0, it follows that
f > 0 for r > a and f < 0 for
r < a; that is, the "normal region" in which t
is time like is outside
the horizon as in the case of, for example, the Schwarzschild metric.
The first term in the left hand side of (184) clearly has the form of
TdS since we have an independent identification of temperature
from the periodicity argument in the local Rindler coordinates.
Since the pressure is P = - Trr,
the right hand side has the structure of PdV or - more
relevantly - is the product of the radial pressure times the transverse
area times the radial displacement. This is important because, for the
metrics in the form (175), the proper transverse area is just that of a
2-sphere though the proper volumes and coordinate volumes differ.
In the case of horizons with B = f'(a) > 0 which
we are considering (with da > 0), the volume of the region
where f < 0 will increase and the volume of the region
where f > 0 will decrease.
Since the entropy is due to the existence of an inaccessible region,
dV must refer to the change in the volume of the inaccessible
region where f < 0. We can now identify
T in TdS and P in PdV without any difficulty
and interpret the remaining term (second term in the left hand side) as
dE = da/2. We thus get the expressions for the entropy
S and energy E (when B > 0) to be
the same as in (179).
Using (184), we can again provide an interpretation of entropy and
energy in the case of de Sitter universe. In this case,
f (r) = (1 - H2 r2),
a = H-1, B = - 2H < 0
so that the temperature - which should be positive - is
T = | f'(a)| /
(4 ) = (- B) /
4
) = (- B) /
4 .
For horizons with B = f'(a) < 0 (like the de
Sitter horizon) which we are now considering,
f (a) = 0, f'(a) < 0, and it follows that
f > 0 for
r < a and f < 0 for r > a;
that is, the "normal region" in which t is time like is inside
the horizon as in the case of, for example, the de Sitter metric.
Multiplying equation (184) by (- 1), we get
.
For horizons with B = f'(a) < 0 (like the de
Sitter horizon) which we are now considering,
f (a) = 0, f'(a) < 0, and it follows that
f > 0 for
r < a and f < 0 for r > a;
that is, the "normal region" in which t is time like is inside
the horizon as in the case of, for example, the de Sitter metric.
Multiplying equation (184) by (- 1), we get
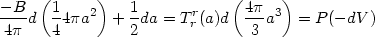 |
(185) |
The first term on the left hand side is again of the form TdS
(with positive temperature and entropy).
The term on the right hand side has the correct sign since the
inaccessible region (where f < 0) is now outside the horizon
and the volume of this region changes by (- dV).
Once again, we can use (185) to identify
[293]
the entropy and the energy:
S = (1/4)(4 a2) = (1/4)Ahorizon; E = -
(1/2)H-1. These results agree with the previous analysis.
a2) = (1/4)Ahorizon; E = -
(1/2)H-1. These results agree with the previous analysis.