2.2. Dynamics of the Friedmann model

Let us now turn to the second assumption which determines the dynamics of the universe. When several non interacting sources are present in the universe, the total energy momentum tensor which appear on the right hand side of the Einstein's equation will be the sum of the energy momentum tensor for each of these sources. Spatial homogeneity and isotropy imply that each T_b^a is diagonal and has the form T_b^a = dia [_i(t), - P_i(t), - P_i(t), - P_i(t)] where the index i = 1, 2,..., N denotes N different kinds of sources (like radiation, matter, cosmological constant etc.). Since the sources do not interact with each other, each energy momentum tensor must satisfy the relation T_b;a^a = 0 which translates to the condition d (_i a³) = - P_i da³. It follows that the evolution of the energy densities of each component is essentially dependent on the parameter w_i (P_i / _i) which, in general, could be a function of time. Integrating d (_i a³) = - w_{i i} da³, we get

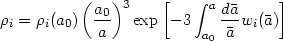(19)

which determines the evolution of the energy density of each of the species in terms of the functions w_i(a).

This description determines (a) for different sources but not a(t). To determine the latter we can use one of the Einstein's equations:

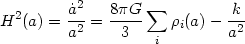(20)

This equation shows that, once the evolution of the individual components of energy density _i(a) is known, the function H(a) and thus the line element in equation (13) is known. (Evaluating this equation at the present epoch one can determine the value of k; hence it is not necessary to provide this information separately.) Given H₀, the current value of the Hubble parameter, one can construct a critical density, by the definition:

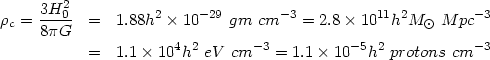(21)

and parameterize the energy density, _i(a₀), of different components at the present epoch in terms of the critical density by _i(a₀) _{i c}. [Observations [49, 50] give h = 0.72 ± 0.03 (statistical) ± 0.07 (systematic)]. It is obvious from equation (20) that k = 0 corresponds to _tot = _{i i} = 1 while _tot > 1 and _tot < 1 correspond to k = ± 1. When _tot 1, equation (20), evaluated at the current epoch, gives (k / a₀²) = H₀²(_tot - 1), thereby fixing the value of (k / a₀²); when, _tot = 1, it is conventional to take a₀ = 1 since its value can be rescaled.