2. FRAMEWORK OF STANDARD COSMOLOGY

All the well developed models of standard cosmology start with two basic assumptions: (i) The distribution of matter in the universe is homogeneous and isotropic at sufficiently large scales. (ii) The large scale structure of the universe is essentially determined by gravitational interactions and hence can be described by Einstein's theory of gravity. The geometry of the universe can then be determined via Einstein's equations with the stress tensor of matter Tⁱ_k(t,x) acting as the source. (For a review of cosmology, see e.g. [43, 44, 45, 46, 47]). The first assumption determines the kinematics of the universe while the second one determines the dynamics. We shall discuss the consequences of these two assumptions in the next two subsections.

2.1. Kinematics of the Friedmann model

The assumption of isotropy and homogeneity implies that the large scale geometry can be described by a metric of the form

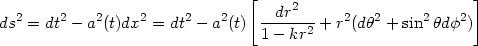(11)

in a suitable set of coordinates called comoving coordinates. Here a(t) is an arbitrary function of time (called expansion factor) and k = 0, ±1. Defining a new coordinate through = (r, sin^-1r, sinh^-1r) for k = (0, + 1, - 1) this line element becomes

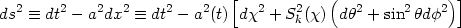(12)

where S_k() = (, sin, sinh) for k = (0, + 1, - 1). In any range of time during which a(t) is a monotonic function of t, one can use a itself as a time coordinate. It is also convenient to define a quantity z, called the redshift, through the relation a(t) = a₀[1 + z(t)]^-1 where a₀ is the current value of the expansion factor. The line element in terms of [a, , , ] or [z, , , ] is:

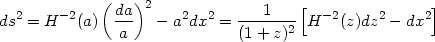(13)

where H(a) = ( / a), called the Hubble parameter, measures the rate of expansion of the universe.

This equation allows us to draw an important conclusion: The only non trivial metric function in a Friedmann universe is the function H(a) (and the numerical value of k which is encoded in the spatial part of the line element.) Hence, any kind of observation based on geometry of the spacetime, however complex it may be, will not allow us to determine anything other than this single function H(a). As we shall see, this alone is inadequate to describe the material content of the universe and any attempt to do so will require additional inputs.

Since the geometrical observations often rely on photons received from distant sources, let us consider a photon traveling a distance r_em(z) from the time of emission (corresponding to the redshift z) till today. Using the fact that ds = 0 for a light ray and the second equality in equation (13) we find that the distance traveled by light rays is related to the redshift by dx = H^-1(z)dz. Integrating this relation, we get

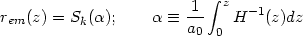(14)

All other geometrical distances can be expressed in terms of r_em(z) (see eg., [44]). For example, the flux of radiation F received from a source of luminosity L can be expressed in the form F = L / (4 d_L²) where

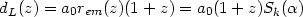(15)

is called the luminosity distance. Similarly, if D is the physical size of an object which subtends an angle to the observer, then - for small - we can define an angular diameter distance d_A through the relation = D / d_A. The angular diameter distance is given by

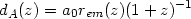(16)

with d_L = (1 + z)² d_A.

If we can identify some objects (or physical phenomena) at a redshift of z having a characteristic transverse size D, then measuring the angle subtended by this object we can determine d_A(z). Similarly, if we have a series of luminous sources at different redshifts having known luminosity L, then by observing the flux from these sources L, one can determine the luminosity distance d_L(z). Determining any of these functions will allow us to use the relations (15) [or (16)] and (14) to obtain H^-1(z). For example, H^-1(z) is related to d_L(z) through

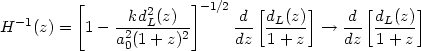(17)

where second equality holds if the spatial sections of the universe are flat, corresponding to k = 0; then d_L(z), d_A(z), r_em(z) and H^-1(z) all contain the (same) maximal amount of information about the geometry.

The function r_em(z) also determines the proper volume of the universe between the redshifts z and z + dz subtending a solid angle d in the sky. The comoving volume element can be expressed in the form

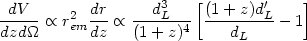(18)

where the prime denotes derivative with respect to z. Based on this, there has been a suggestion [48] that future observations of the number of dark matter halos as a function of redshift and circular velocities can be used to determine the comoving volume element to within a few percent accuracy. If this becomes possible, then it will provide an additional handle on constraining the cosmological parameters.

The above discussion illustrates how cosmological observations can be used to determine the metric of the spacetime, encoded by the single function H^-1(z). This issue is trivial in principle, though enormously complicated in practice because of observational uncertainties in the determination of d_L(z), d_A(z) etc. We shall occasion to discuss these features in detail later on.