7.4. Anthropic interpretation of the cosmological constant

The anthropic principle [264, 265] is an interpretational paradigm which argues that, while discussing the origin of physical phenomena and the values of constants of nature, we must recognize the fact that only certain combination and range of values will lead to the existence of intelligence observers in the universe who could ask questions related to these issues. This paradigm has no predictive power in the sense that none of the values of the cosmological parameters were ever predicted by this method. ⁽¹⁾ In fact some cosmologists have advocated the model with _NR = 1, = 0 strongly and later - when observations indicated 1 - have advocated the anthropic interpretation of cosmological constant with equal fluency. This is defended by the argument that not all guiding principles in science (Darwinian evolution, Plate tectonics, ....) need to be predictive in order to be useful. In this view point, anthropic principle is a back drop for discussing admittedly complicated conceptual issues. Within this paradigm there have been many attempts to explain (after the fact) the values of several fundamental constants with varying degree of success.

In the context of cosmological constant, the anthropic interpretation works as follows. It is assumed that widely disparate values for the constants of nature can occur in an ensemble of universes (or possibly in different regions of the universe causally unconnected with each other). Some of these values for constants of nature - and in particular for the cosmological constant - will lead broadly to the kind of universe we seem to live in. This is usually characterized by formation of: (i) structures by gravitational instability, (ii) stars which act as gravitationally bound nuclear reactors that synthesize the elements and distribute them and (iii) reasonably complex molecular structures which could form the basis for some kind of life form. Showing that such a scenario can exist only for a particular range of values for the cosmological constant is considered an explanation for the value of cosmological constant by the advocates of anthropic principle. (More sophisticated versions of this principle exist; see, for example [266], and references cited therein.)

The simplest constraint on the cosmological constant is that it should not be so high as to cause rapid expansion of the universe early on preventing the formation of galaxies [267]. If the energy density of the cosmological constant has to be less than that of energy density of matter at the redshift z_gal( 4) at which galaxy formation takes place, then we must have

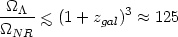(115)

This gives a bound on which is "only" a couple of orders of magnitude larger than what is observed.

More formally, one could ask: What is the most probable value of if it is interpreted as the value that would have been observed by the largest number of observers [268, 269]? Since a universe with _NR will have more galaxies than one with a universe with 10² _NR, one could argue that most observers will measure a value _NR. 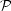The actual probability dP for measuring a particular value for in the range (, + d) is the product (dP / d) = Q() () where 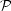is the a priori probability measure for a specific value of in a member of an ensemble of universes (or in a region of the universe) and Q() is the average number of galaxies which form in a universe with a given value of . There has been several attempts to estimate these quantities (see, for example, [270, 271]) but all of them are necessarily speculative. 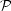The first - and the most serious - difficulty with this approach is the fact that we simply do not have any reliable way of estimating ; in fact, if we really had a way of calculating it from a fundamental theory, such a theory probably would have provided a deeper insight into the cosmological constant problem itself. The second issue has to do with the dependence of the results on other parameters which describe the cosmological structure formation (like for example, the spectrum of initial perturbations). To estimate Q one needs to work in a multi parameter space and marginalize over other parameters - which would involve more assumptions regarding the priors. And finally, anthropic paradigm itself is suspect in any scientific discussion, for reasons mentioned earlier.

¹ Some advocates of the anthropic principle cite Fred Hoyle predicting the existence of excited state of carbon nucleus, thereby leading to efficient triple alpha reaction in stellar nucleosynthesis, as an example of a prediction from anthropic principle; it is very doubtful whether Hoyle applied anthropic considerations in arriving at this conclusion. Back.