7.3. Cosmological constant as a stochastic variable

Current cosmological observations can be interpreted as showing that the effective value value of (which will pick up contributions from all vacuum energy densities of matter fields) has been reduced from the natural value of L_P^-2 to L_P^-2(L_P H₀)² where H₀ is the current value of the Hubble constant. One possible way of thinking about this issue is the following [261]: Let us assume that the quantum micro structure of spacetime at Planck scale is capable of readjusting itself, soaking up any vacuum energy density which is introduced - like a sponge soaking up water. If this process is fully deterministic and exact, all vacuum energy densities will cease to have macroscopic gravitational effects. However, since this process is inherently quantum gravitational, it is subject to quantum fluctuations at Planck scales. Hence, a tiny part of the vacuum energy will survive the process and will lead to observable effects. One may conjecture that the cosmological constant we measure corresponds to this small residual fluctuation which will depend on the volume of the spacetime region that is probed. It is small, in the sense that it has been reduced from L_P^-2 to L_P^-2(L_P H₀)², which indicates the fact that fluctuations - when measured over a large volume - is small compared to the bulk value. It is the wetness of the sponge we notice, not the water content inside.

This is particularly relevant in the context of standard discussions of the contribution of zero-point energies to cosmological constant. The correct theory is likely to regularise the divergences and make the zero point energy finite and about L_P^-4. This contribution is most likely to modify the microscopic structure of spacetime (e.g if the spacetime is naively thought of as due to stacking of Planck scale volumes, this will modify the stacking or shapes of the volume elements) and will not affect the bulk gravitational field when measured at scales coarse grained over sizes much bigger than the Planck scales.

Given a large 4-volume of the spacetime, we will divide it into M cubes of size ( x)⁴ and label the cubes by n = 1, 2,....., M. The contribution to the path integral amplitude 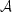, describing long wavelength limit of conventional Einstein gravity, can be expressed in the form

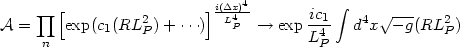(107)

where we have indicated the standard continuum limit. (In conventional units c₁ = (16)^-1.) Let us now ask how one could modify this result to describe the ability of spacetime micro structure to readjust itself and absorb vacuum energy densities. This would require some additional dynamical degree of freedom that will appear in the path integral amplitude and survive in the classical limit. It can be shown that [261] the simplest implementation of this feature is by modifying the standard path integral amplitude [exp(c₁(R L_P²) + ^... )] by a factor [(x_n) / ₀] where (x) is a scalar degree of freedom and ₀ is a pure number introduced to keep this factor dimensionless. In other words, we modify the path integral amplitude to the form:

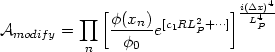(108)

In the long wavelength limit, the extra factor in (108) will lead to the term of the form

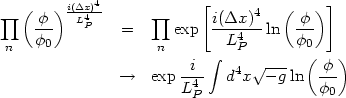(109)

Thus, the net effect of our assumption is to introduce a `scalar field potential' V() = - L_P^-4 ln( / ₀) in the semi classical limit. It is obvious that the rescaling of such a scalar field by q is equivalent to adding a cosmological constant with vacuum energy - L_P^-4ln q. Alternatively, any vacuum energy can be re absorbed by such a rescaling. The fact that the scalar degree of freedom occurs as a potential in (109) without a corresponding kinetic energy term shows that its dynamics is unconventional and non classical.

The above description in terms of macroscopic scalar degree of freedom can, of course, be only approximate. Treated as a vestige of a quantum gravitational degrees of freedom, the cancellation cannot be precise because of fluctuations in the elementary spacetime volumes. These fluctuations will reappear as a "small" cosmological constant because of two key ingredients: (i) discrete spacetime structure at Planck length and (ii) quantum gravitational uncertainty principle.

To show this, we use the fact noted earlier in section 7.1 that the net cosmological constant can be thought of as a Lagrange multiplier for proper volume of spacetime in the action functional for gravity. In any quantum cosmological models which leads to large volumes for the universe, phase of the wave function will pick up a factor of the form

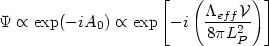(110)

from (104), where is the four volume. Treating (_eff / 8 L_P², ) as conjugate variables (q, p), we can invoke the standard uncertainty principle to predict 8 L_P² / . Now we use the earlier assumption regarding the microscopic structure of the spacetime: Assume that there is a zero point length of the order of L_P so that the volume of the universe is made of a large number (N) of cells, each of volume ( L_P)⁴ where is a numerical constant. Then = N( L_P)⁴, implying a Poisson fluctuation ( L_P)² and leading to

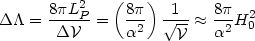(111)

This will give = (8 / 3²) which will - for example - lead to = (2/3) if = 2 . Thus Planck length cutoff (UV limit) and volume of the universe (IR limit) combine to give the correct . (A similar result was obtained earlier in [260] based on a different model.) The key idea, in this approach, is that is a stochastic variable with a zero mean and fluctuations. It is the rms fluctuation which is being observed in the cosmological context.

This has three implications: First, FRW equations now need to be solved with a stochastic term on the right hand side and one should check whether the observations can still be explained. The second feature is that stochastic properties of need to be described by a quantum cosmological model. If the quantum state of the universe is expanded in terms of the eigenstates of some suitable operator (which does not commute the total four volume operator), then one should be able to characterize the fluctuations in each of these states. Third, and most important, the idea of cosmological constant arising as a fluctuation makes sense only if the bulk value is rescaled away.

The non triviality of this result becomes clear when we compare it with few other alternative ways of estimating the fluctuations - none of which gives the correct result. The first alternative approach is based on the assumption that one can associate an entropy S = (A_H / 4L_P²) with compact space time horizons of area A_H (We will discuss this idea in detail in section 10). A popular interpretation of this result is that horizon areas are quantized in units of L_P² so that S is proportional to the number of bits of information contained in the horizon area. In this approach, horizon areas can be expressed in the form A_H = A_PN where A_P L_P² is a quantum of area and N is an integer. Then the fluctuations in the area will be A_H = A_P N =(A_P A_H)^1/2. Taking A_H ^-1 for the de Sitter horizon, we find that H²(H L_P) which is a lot smaller than what one needs. Further, taking A_H r_H², we find that r_H L_P; that is, this result essentially arises from the idea that the radius of the horizon is uncertain within one Planck length. This is quite true, of course, but does not lead to large enough fluctuations.

A more sophisticated way of getting this (wrong) result is to relate the fluctuations in the cosmological constant to that of the volume of the universe is by using a canonical ensemble description for universes of proper Euclidean 4-volume [262]. Writing V / 8 L_P² and treating V and as the relevant variables, one can write a partition function for the 4-volume as

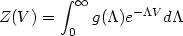(112)

Taking the analogy with standard statistical mechanics (with the correspondence V and E), we can evaluate the fluctuations in the cosmological constant in exactly the same way as energy fluctuations in canonical ensemble. (This is done in several standard text books; see, for example, [263] p. 194.) This will give

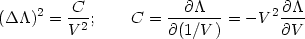(113)

where C is the analogue of the specific heat. Taking the 4-volume of the universe to be = bH^-4 = 9b ^-2 where b is a numerical factor and using V = ( / 8 L_P²) we get L_P^-1 V^-1/2. It follows from (113) that

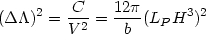(114)

In other words H²(HL_P), which is the same result from area quantization and is a lot smaller than the cosmologically significant value.

Interestingly enough, one could do slightly better by assuming that the horizon radius is quantized in units of Planck length, so that r_H = H^-1 = NL_P. This will lead to the fluctuations r_H = (r_H L_P)^1/2 and using r_H = H^{-1 -1/2}, we get H²(HL_P)^1/2 - larger than (114) but still inadequate. In summary, the existence of two length scales H^-1 and L_P allows different results for depending on how exactly the fluctuations are characterized (V N, A N or r_H N). Hence the result obtained above in (111) is non trivial.

These conclusions stress, among other things, the difference between fluctuations and the mean values. For, if one assumes that every patch of the universe with size L_P contained an energy E_P, then a universe with characteristic size H^-1 will contain the energy E = (E_P / L_P)H^-1. The corresponding energy density will be _V = (E/H^-3) = (H / L_P)² which leads to the correct result. But, of course, we do not know why every length scale L_P should contain an energy E_P and - more importantly - contribute coherently to give the total energy.