8. RELAXATION MECHANISMS FOR THE COSMOLOGICAL CONSTANT

One possible way of obtaining a small, non-zero, cosmological constant at the present epoch of the universe is to make the cosmological constant evolve in time due to some physical process. At a phenomenological level this can be done either by just postulating such a variation and explore its consequences or - in a slightly more respectable way - by postulating a scalar field potential as described in section 4. These models, however, cannot explain why a bare cosmological constant [the first term on the right hand side of (7)] is zero. To tackle this issue, one can invoke some field [usually a scalar field] which directly couples to the cosmological constant and decreases its "effective value". We shall now examine two such models.

The key idea is to introduce a field which couples to the trace T = T^a_a of the energy momentum tensor. If T depends on and vanishes at some value = ₀, then will evolve towards = ₀ at which T = 0. This equilibrium solution will have zero cosmological constant [276, 277, 278, 279]. While this idea sounds attractive, there are general arguments as to why it does not work in the simplest context [4].

A related attempt was made by several authors, [276, 280, 281], who coupled the scalar field directly to R which, of course, is proportional to T because of Einstein's equations. Generically, these models have the Lagrangian

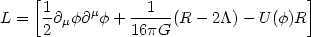(116)

The field equations of this model has flat spacetime solutions at = ₀ provided U(₀) = . Unfortunately, the effective gravitational constant in this model evolves as

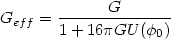(117)

and vanishes as U . Hence these models are not viable.

The difficulty in these models arise because they do not explicitly couple the trace of the T_ab of the scalar field itself. Handling this consistently [282] leads to a somewhat different model which we will briefly describe because of its conceptual interest.

Consider a system consisting of the gravitational fields g_ab, radiation fields, and a scalar field which couples to the trace of the energy-momentum tensor of all fields, including its own. The zeroth order action for this system is given by

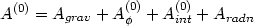(118)

where

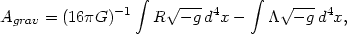	(119)
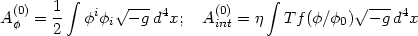	(120)

Here, we have explicitly included the cosmological constant term and is a dimensionless number which `switches on' the interaction. In the zeroth order action, T represents the trace of all fields other than . Since the radiation field is traceless, the only zeroth-order contribution to T comes from the term, so that we have T = 4. The coupling to the trace is through a function f of the scalar field, and one can consider various possibilities for this function. The constant ₀ converts to a dimensionless variable, and is introduced for dimensional convenience.

To take into account the back-reaction of the scalar field on itself, we must add to T the contribution T = - ¹ ₁ of the scalar field. If we now add T to T in the interaction term A_int⁽⁰⁾ further modifies T^ik. This again changes T. Thus to arrive at the correct action an infinite iteration will have to be performed and the complete action can be obtained by summing up all the terms. (For a demonstration of this iteration procedure, see [283, 284].) The full action can be found more simply by a consistency argument.

Since the effect of the iteration is to modify the expression for A and A, we consider the following ansatz for the full action:

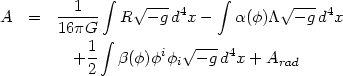(121)

Here () and () are functions of to be determined by the consistency requirement that they represent the effect of the iteration of the interaction term. (Since radiation makes no contribution to T, we expect A_rad to remain unchanged.) The energy-momentum tensor for and is now given by

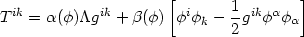(122)

so that the total trace is T_tot = 4() - () ⁱ _i. The functions () and () can now be determined by the consistency requirement

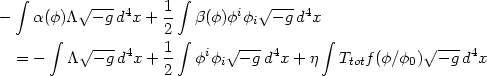(123)

Using T_tot and comparing terms in the above equation we find that

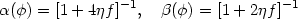(124)

Thus the complete action can be written as

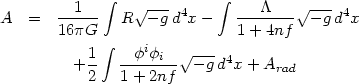(125)

(The same action would have been obtained if one uses the iteration procedure.) The action in (125) leads to the following field equations,

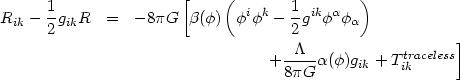	(126)
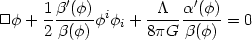	(127)

Here, stands for a covariant d'Lambertian, T_ik^traceless is the stress tensor of all fields with traceless stress tensor and a prime denotes differentiation with respect to .

In the cosmological context, this reduces to

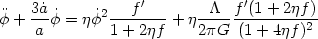	(128)
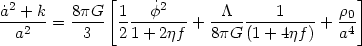	(129)

It is obvious that the effective cosmological constant can decrease if f increases in an expanding universe.The result can be easily generalized for a scalar field with a potential by replacing by V(). This model is conceptually attractive since it correctly accounts for the coupling of the scalar field with the trace of the stress tensor.

The trouble with this model is two fold: (a) If one uses natural initial conditions and do not fine tune the parameters, then one does not get a viable model. (b) Since the scalar field couples to the trace of all sources, it also couples to dust-like matter and "kills" it, making the universe radiation dominated at present. This reduces the age of the universe and could also create difficulties for structure formation. These problems can be circumvented by invoking a suitable potential V() within this model [285]. However, such an approach takes away the naturalness of the model to certain extent.