4. MODELS WITH EVOLVING COSMOLOGICAL "CONSTANT"

The observations which suggest the existence of non-zero cosmological constant - discussed in the last section - raises serious theoretical problems which we mentioned in section 1.1. These difficulties have led people to consider the possibility that the dark energy in the universe is not just a cosmological constant but is of more complicated nature, evolving with time. Its value today can then be more naturally set by the current expansion rate rather than predetermined earlier on - thereby providing a solution to the cosmological constant problems.

Though a host of models have been constructed based on this hope, none of them provides a satisfactory solution to the problems of fine-tuning. Moreover, all of them involve an evolving equation of state parameter w_X(a) for the unknown ("X") dark energy component, thereby taking away all predictive power from cosmology [165]. Ultimately, however, this issue needs to settled observationally by checking whether w_X(a) is a constant [equal to -1, for the cosmological constant] at all epochs or whether it is indeed varying with a. We shall now discuss several observational and theoretical issues connected with this theme.

While the complete knowledge of the T_b^a [that is, the knowledge of the right hand side of (20)] uniquely determines H(a), the converse is not true. If we know only the function H(a), it is not possible to determine the nature of the energy density which is present in the universe. We have already seen that geometrical measurements can only provide, at best, the functional form of H(a). It follows that purely geometrical measurements of the Friedmann universe will never allow us to determine the material content of the universe.

[The only exception to this rule is when we assume that each of the components in the universe has constant w_i. This is fairly strong assumption and, in fact, will allow us to determine the components of the universe from the knowledge of the function H(a). To see this, we first note that the term (k/a²) in equation (22) can be thought of as contributed by a hypothetical species of matter with w = - (1/3). Hence equation (22) can be written in the form

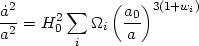(41)

with a term having w_i = - (1/3) added to the sum. Let 3(1 + w) and () denote the fraction of the critical density contributed by matter with w = (/3) - 1. (For discrete values of w_i and _i, the function () will be a sum of Dirac delta functions.) In the continuum limit, equation (41) can be rewritten as

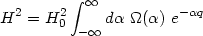(42)

where (a/a₀) = exp(q). The function () is assumed to have finite support (or decrease fast enough) for the expression on the right hand side to converge. If the observations determine the function H(a), then the left hand side can be expressed as a function of q. An inverse Laplace transform of this equation will then determine the form of () thereby determining the composition of the universe, as long as all matter can be described by an equation of state of the form p_i = w_{i i} with w_i = constant for all i = 1,...., N.]

More realistically one is interested in models which has a complicated form of w_X(a) for which the above analysis is not applicable. Let us divide the source energy density into two components: _k(a), which is known from independent observations and a component _X(a) which is not known. From (20), it follows that

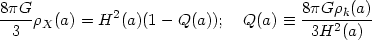(43)

Taking a derivative of ln_X(a) and using (19), it is easy to obtain the relation

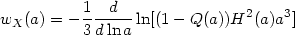(44)

If geometrical observations of the universe give us H(a) and other observations give us _k(a) then one can determine Q and thus w_X(a). While this is possible, in principle the uncertainties in measuring both H and Q makes this a nearly impossible route to follow in practice. In particular, one is interested in knowing whether w evolves with time or a constant and this turns out to be a very difficult task observationally. We shall now briefly discuss some of the issues.