3. THE COSMOLOGICAL CONSTANT

In 1915 Albert Einstein introduced his theory of General Relativity. Like Newton before him, Einstein's desire was to apply his theory to cosmology. Einstein embraced the prevailing view at that time that the universe is static. Therefore, he attempted to find solutions of the form = 0. It soon became apparent that even with Einstein's theory of gravity, as with Newton's, the gravitational attraction of the matter in the universe causes a static universe to be unstable. Furthermore, as can be seen from Eq. (4), the subsequent requirement of = 0 implies a negative pressure such that p = - / 3. For ordinary stellar matter and gas, this relationship is not physically reasonable.

To remedy such problems, Einstein modified his original field equations from Eq. (2) to the more general form

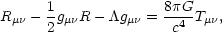(12)

where is the cosmological constant mentioned in the previous section. Equation (12) is the most general form of the field equations that remains consistent with the physical requirements of a relativistic theory of gravity. The cosmological constant term, for > 0, can be viewed as a repulsive form of gravity that is independent of the curvature of spacetime. The modern approach is to treat as a form of energy present even in empty space - vacuum energy. [5] This interpretation implies modifying Eq. (12) to

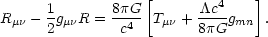(13)

In the perfect fluid approximation, this leads to an effective fluid pressure and energy density given by

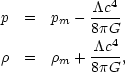(14) (15)

where p_m and _m are the pressure and energy density of the matter content of the universe. As Eq. (14) shows, the cosmological constant contributes a negative term to the pressure in the universe. This affect of the cosmological constant allowed Einstein to find a static, albeit unstable, solution for the dynamics of the universe.

Once it became known that the universe is expanding, Einstein discarded the cosmological constant term having no other physical reason to include it. However, the possible existence of a non-zero cosmological constant has been a subject of debate ever since. With the cosmological constant in the picture, the equations for the dynamics of the universe, Eqs. (4) and (5), generalize to

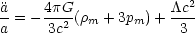(16)

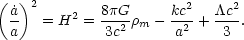(17)

Besides Einstein's static model of the universe, another interesting, and important, solution to Eqs. (16) and (17), known as the de Sitter solution, applies to the case of a spatially flat, empty universe (_m = 0, p_m = 0, k = 0). In this case, supplies the only contribution to the energy density

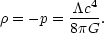(18)

Equation (16) shows that under these conditions the universe would be accelerating > 0, and Eq. (17) shows that the Hubble parameter would be given by

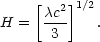(19)

The de Sitter solution for the cosmic scale factor shows that the effect of the cosmological constant is to cause the accelerating universe to expand exponentially with time according to

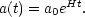(20)

Obviously, the universe is not completely empty, but the de Sitter solution remains important because it is possible for a cosmological constant term to be sufficiently large as to dominate the dynamics of the universe. The dominant components of the universe are determined by the relative values of the corresponding density parameters. Dividing Eq. (17) by H² produces the analog of Eq. (7)

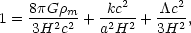(21)

where the sign of k has be separated out. The first term on the right-hand-side is called the matter term and, in analogy with Eq. (8), also gives the matter density parameter _m. The second term is the curvature term and is characterized by the curvature density parameter _k. Finally, the last term is known as the vacuum-energy density parameter . Thus, in a universe with a cosmological constant, the primary density parameters are

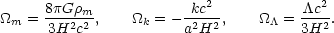(22)

The present values of these parameters, together with the Hubble constant, would determine the dynamics of the universe in this model. [6]