


Throughout their lives, stars remain in stable (hydrostatic) equilibrium due to the balance between outward pressures (from the fluid and radiation) and the inward pressure due to the gravitational force. The enormously energetic nuclear fusion that occurs in stellar cores causes the outward pressure. The weight of the outer region of the star causes the inward pressure. A supernova occurs when the gravitational pressure overcomes the internal pressure, causing the star to collapse, and then violently explode. There is so much energy released (in the form of light) that we can see these events out to extremely large distances.
Supernovae are classified into two types according to their spectral features and light curves (plot of luminosity vs. time). Specifically, the spectra of type Ia supernovae are hydrogen-poor, and their light curves show a sharp rise with a steady, gradual decline. In addition to these spectroscopic features, the locations of these supernovae, and the absence of planetary nebulae, allow us to determine the genesis of these events. Based on these facts, it is believed that the progenitor of a type Ia supernova is a binary star system consisting of a white dwarf with a red giant companion. [7] Other binary systems have been theorized to cause these supernovae, but are not consistent with spectroscopic observation. [8]
Although the Sun is not part of a binary system, approximately half of all stellar systems are. Both members are gravitationally bound and therefore revolve around each other. While a binary star system is very common, the members of the progenitor to a type Ia supernova have special properties. White dwarf stars are different from stars like the Sun in that nuclear fusion does not take place within these objects. Electron degeneracy pressure, which is related to the well known Pauli exclusion principle, holds the white dwarf up against its own weight. For electron degeneracy pressure to become important, an object must be extremely dense. White dwarf stars have the mass of the Sun, but are the size of the Earth. Also, the physics of this exotic form of pressure produces a strange effect: heavier white dwarfs are actually smaller in size (Mass × Volume = Constant). [9] Red giant stars, on the other hand, are the largest known stars and contain a relatively small amount of mass. As a result, gravity is relatively weak at the exterior region of red giant stars.
In such a binary system, the strong gravitational attraction of the white dwarf overcomes the weaker gravity of the red giant. At the outer edge of the red giant, the gravitational force from the white dwarf is stronger than that from the red giant. This causes mass from the outer envelope of the red giant to be accreted onto the white dwarf. As a result, the mass of the white dwarf increases, causing its size to decrease. This process continues until the mass of the white dwarf reaches the Chandrasekhar limit (1.44 solar masses) beyond which electron degeneracy pressure is no longer able to balance the increasing pressure due to the gravitational force. At the center of the white dwarf, the intense pressure and temperature ignites the fusion of Carbon nuclei. This sudden burst of energy produces an explosive deflagration (subsonic) wave that destroys the star. This violently exploding white dwarf is what we see as a type Ia supernova.
The use of type Ia supernovae for determining cosmological parameters rests on the ability of these supernovae to act as standard candles. Standard candles have been used to determine distances to celestial objects for many years. They are luminous objects whose intrinsic (or absolute) brightness can be determined independent of their distance. The intrinsic brightness, together with the observed apparent brightness (which depends on the distance to the object), can be used to calculate distances. The distance calculated from measurements of the luminosity (power output) of an object is appropriately termed the luminosity distance
 |
(23) |
where m is the apparent brightness measured in magnitudes (apparent magnitude), M is the absolute magnitude, and d is the luminosity distance in units of megaparsecs. The quantity, m - M is commonly known as the distance modulus. For the reader who is unfamiliar with the magnitude scale see chapter 3 of Ref. 9.
As explained above, all type Ia supernovae are caused by the same process, a white dwarf reaching 1.44 solar masses by accretion from a red giant. As a result of this consistency, we not only expect to see extremely consistent light curves from these events, but we also expect that these light curves will reach the same peak magnitude. If this latter point is true, type Ia supernovae can be used as standard candles and, therefore, distance indicators.
Methods for determining the absolute magnitude of a type Ia supernova can be divided into two categories depending on whether or not we know the distance to the event. If we know the distance to the host galaxy of the supernova, by means of a Cepheid variable for example, and we observe the apparent magnitude of the event m, then we can use the distance modulus to calculate the absolute magnitude directly
 |
(24) |
If the distance is not known, the peak luminosity must be inferred from observational data. The techniques for making this inference often involve corrections for many processes that would otherwise adversely affect the results. These processes include interstellar extinction within the host galaxy, redshift of the light from the expansion of the universe, gravitational lensing, and an apparently natural scatter in the peak brightness; see Ref. 10 for a discussion of these corrections. Once the luminosity L of a supernova has been determined, this luminosity, together with the luminosity L' and absolute magnitude M' , of a well-known object (such as the Sun) will yield the absolute magnitude of the supernova
 |
(25) |
Taking all of this into account, it has been determined that the peak absolute magnitude of type Ia supernovae is. [11]
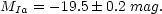 |
(26) |